The side of a rectangle are 6.01 m and 12 m Taking the significant figures into account , the area of the rectangle is
7.2m2
72.1m2
72m2
72.12m2
The correct Answer is:C
To find the area of a rectangle given its sides, we follow these steps:
1. Identify the dimensions of the rectangle:
- Length (L) = 12 m
- Breadth (B) = 6.01 m
2. Calculate the area using the formula:
- Area (A) = Length × Breadth
- A = 12 m × 6.01 m
3. Perform the multiplication:
- A = 12 × 6.01 = 72.12 m²
4. Determine the significant figures:
- The length (12 m) has 2 significant figures.
- The breadth (6.01 m) has 3 significant figures.
- According to the rules of significant figures in multiplication, the result should be reported with the same number of significant figures as the measurement with the least number of significant figures, which in this case is 2 significant figures.
5. Round the area to the correct number of significant figures:
- The calculated area is 72.12 m². Rounding this to 2 significant figures gives us 72 m².
Final Answer:
The area of the rectangle, taking significant figures into account, is 72 m².
---
- Length (L) = 12 m
- Breadth (B) = 6.01 m
- Area (A) = Length × Breadth
- A = 12 m × 6.01 m
- A = 12 × 6.01 = 72.12 m²
- The length (12 m) has 2 significant figures.
- The breadth (6.01 m) has 3 significant figures.
- According to the rules of significant figures in multiplication, the result should be reported with the same number of significant figures as the measurement with the least number of significant figures, which in this case is 2 significant figures.
- The calculated area is 72.12 m². Rounding this to 2 significant figures gives us 72 m².
The area of the rectangle, taking significant figures into account, is 72 m².
Similar Questions
The sides of a rectangle are 7.01 m and 1.2×101m. Taking the significant figures into account, the area of the rectangle is
View SolutionThe side of a rectangle is 6 more than its breadth. If the breadth is a, find the rule for finding the area of the rectangle. If the breadth of the rectangle is 8 cm, find its area.
View Solution
Knowledge Check
The average length of all the sides of a rectangle equals twice the width of the rectangle. If the area of the rectangle is 18, what is its perimeter?
A6√6B8√6C24D32
The area of a rectangle is 640 m2. Taking its length as x m, find, in term of x, the width of the rectangle. If the perimeter of the rectangle is 104 m, find its dimensions.
View SolutionThe are of a square is the same as that of a rectangle. If the side of a square is 60 m and the breadth of the rectangle is 48 m, find the length of the rectangle.
View SolutionThe measurements of the sides of a rectangle are given. Find
(i) the value of x.
(ii) the area of the rectangle
(iii) the perimeter of the rectangle .
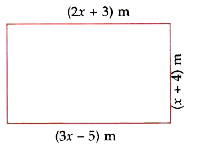
View SolutionThe length of a rectangle is 8 cm more than the breadth. If the perimeter of the rectangle is 80 cm, then the area of the rectangle is (a)192 cm2 (b) 364 cm2 (c)384 cm2 (d) 382 cm2
View Solution(i) The two sides of a rectangle are x units and (10 - x) units. For what value of x, the area of rectangle will be maximum?
(ii) Prove that a rectangle, whose area is constant has minimum perimeter if it is a square.
View SolutionA wire is in the form of a square of side 18 m. It is bent in the form of a rectangle, whose length and breadth are in the ratio 3:1. The area of the rectangle is
(a) 81 m2
(b) 243 m2
(c) 144 m2
(d) 324 m2
View SolutionThe area of a square and a rectangle are equal. If the side of the square is40 cm and the breadth of the rectangle is 25 cm, find the length of therectangle. Also, find the perimeter of the rectangle.
View Solution
