When a monochromatic light ray is incident on a medium of refracive indexwith angle of incidence ,the angle of refraction is if is changed slightly by,then the corresponding change in will be-
The correct Answer is:C
To solve the problem, we need to relate the change in the angle of refraction Δθr to the change in the angle of incidence Δθi using Snell's Law.
1. Start with Snell's Law:
Snell's Law states that:
μ=sinθisinθr
where μ is the refractive index, θi is the angle of incidence, and θr is the angle of refraction.
2. Rearranging Snell's Law:
From Snell's Law, we can express sinθr in terms of θi:
sinθr=1μsinθi
3. Differentiate with respect to θi:
We differentiate both sides with respect to θi:
cosθrdθrdθi=1μcosθi
4. Express dθr in terms of dθi:
Rearranging the above equation gives:
dθrdθi=1μcosθicosθr
5. Relate changes Δθr and Δθi:
If we denote small changes in angles as Δθi and Δθr, we can write:
Δθr=1μcosθicosθrΔθi
6. Final Expression:
Thus, the change in the angle of refraction Δθr corresponding to a change in the angle of incidence Δθi is given by:
Δθr=1μcosθicosθrΔθi
Conclusion:
The final expression for the change in the angle of refraction Δθr is:
Δθr=1μcosθicosθrΔθi
Snell's Law states that:
μ=sinθisinθr
where μ is the refractive index, θi is the angle of incidence, and θr is the angle of refraction.
From Snell's Law, we can express sinθr in terms of θi:
sinθr=1μsinθi
We differentiate both sides with respect to θi:
cosθrdθrdθi=1μcosθi
Rearranging the above equation gives:
dθrdθi=1μcosθicosθr
If we denote small changes in angles as Δθi and Δθr, we can write:
Δθr=1μcosθicosθrΔθi
Thus, the change in the angle of refraction Δθr corresponding to a change in the angle of incidence Δθi is given by:
Δθr=1μcosθicosθrΔθi
The final expression for the change in the angle of refraction Δθr is:
Δθr=1μcosθicosθrΔθi
Similar Questions
A ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View SolutionA ray of light passes from glass, having a refractive index of 1.6, to air. The angle of incidence for which the angle of refraction is twice the angle of incidence is
View SolutionA ray of monochromatic light is incident on the plane surface of separation between two media x and y with angle of incidence i in the medium x and angle of refraction r in the medium y. The graph shows the relation between sin i and sin r.

View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
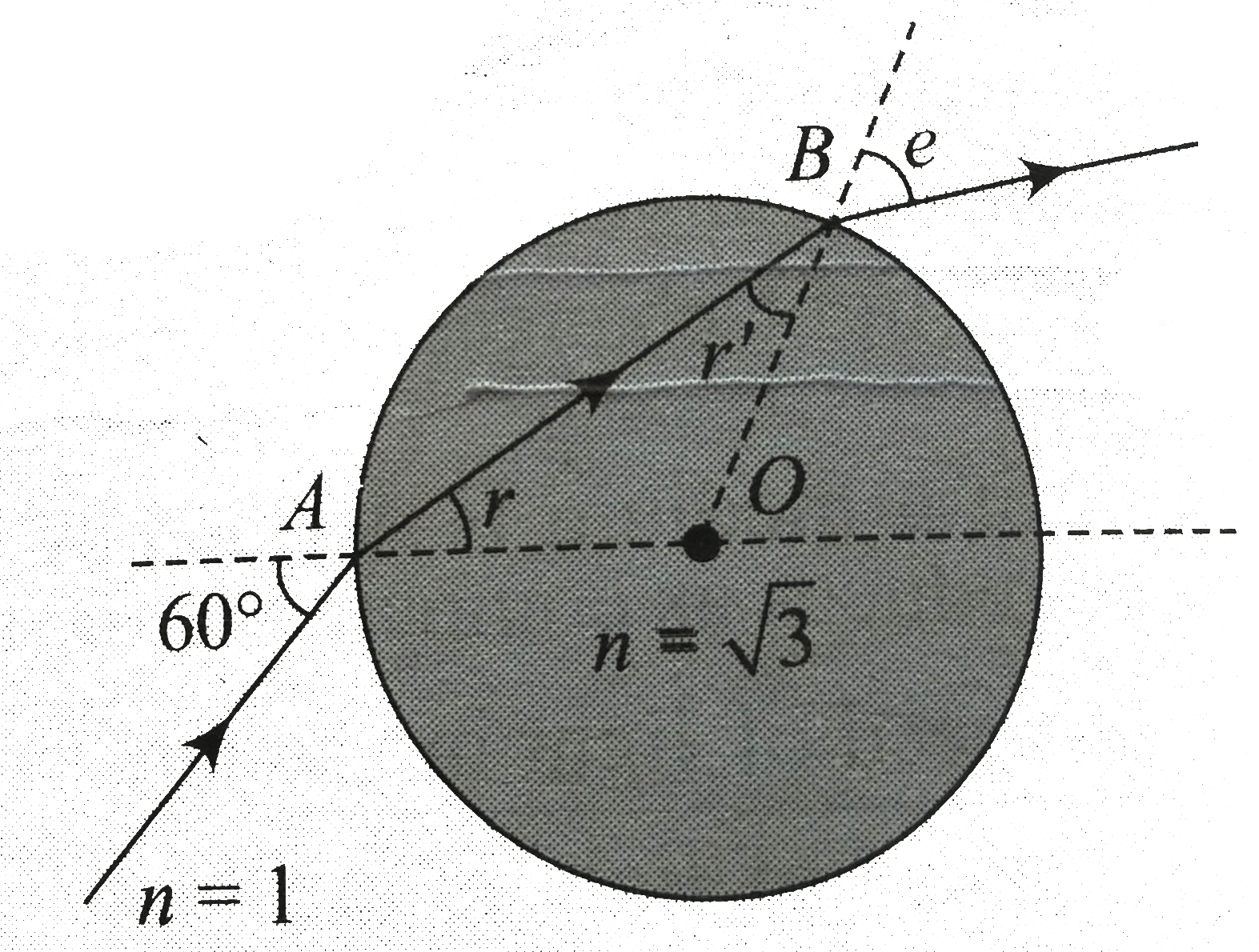
View SolutionA light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r,r1,e and the total deviation after two refractions.

View Solution
