A disc of mass 4.8 kg and radius 1 m is rolling on a horizontal surface without sliding with angular velocity of 600 rotations/min. What is the total kinetic energy of the disc ?
360 J
1440π2J
4000π2J
600π2J
The correct Answer is:A
To solve the problem of finding the total kinetic energy of a disc rolling without slipping, we can break down the solution into several steps:
Step 1: Understand the Problem
We have a disc with a mass m=4.8kg and radius r=1m rolling on a horizontal surface without slipping. The angular velocity is given as 600rotations/min.
Step 2: Convert Angular Velocity to Radians per Second
First, we need to convert the angular velocity from rotations per minute to radians per second.
Angular velocity(ω)=600rotations/min×2πradians1rotation×1min60s
Calculating this gives:
ω=600×2π60=10×2π=20πradians/s
Step 3: Determine the Linear Velocity
Since the disc is rolling without slipping, the linear velocity V can be calculated using the relationship:
V=ω⋅r
Substituting the values:
V=20π⋅1=20πm/s
Step 4: Calculate the Translational Kinetic Energy
The translational kinetic energy (KEtrans) is given by the formula:
KEtrans=12mV2
Substituting the values:
KEtrans=12⋅4.8⋅(20π)2
Calculating (20π)2:
(20π)2=400π2
Thus,
KEtrans=12⋅4.8⋅400π2=960π2J
Step 5: Calculate the Rotational Kinetic Energy
The rotational kinetic energy (KErot) for a disc is given by:
KErot=12Iω2
For a disc, the moment of inertia I is:
I=12mr2
Substituting the values:
I=12⋅4.8⋅(1)2=2.4kg m2
Now substituting I and ω:
KErot=12⋅2.4⋅(20π)2
Calculating this:
KErot=12⋅2.4⋅400π2=480π2J
Step 6: Calculate Total Kinetic Energy
The total kinetic energy (KEtotal) is the sum of the translational and rotational kinetic energies:
KEtotal=KEtrans+KErot=960π2+480π2=1440π2J
Final Answer
The total kinetic energy of the disc is:
1440π2J
We have a disc with a mass m=4.8kg and radius r=1m rolling on a horizontal surface without slipping. The angular velocity is given as 600rotations/min.
First, we need to convert the angular velocity from rotations per minute to radians per second.
Since the disc is rolling without slipping, the linear velocity V can be calculated using the relationship:
The translational kinetic energy (KEtrans) is given by the formula:
The rotational kinetic energy (KErot) for a disc is given by:
The total kinetic energy (KEtotal) is the sum of the translational and rotational kinetic energies:
The total kinetic energy of the disc is:
Similar Questions
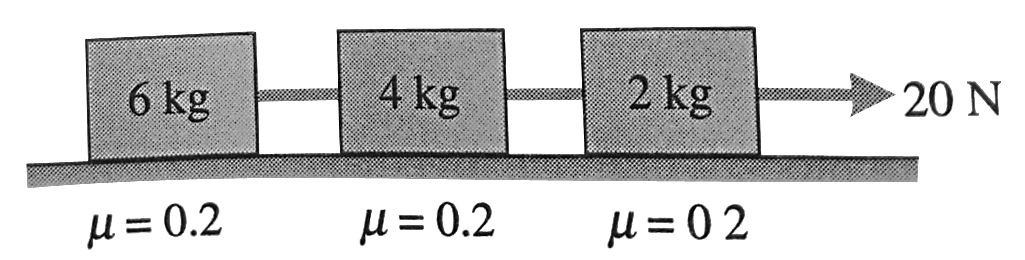
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View SolutionA solid sphere rolls on horizontal surface without slipping. What is the ratio of its rotational to translation kinetic energy.
View Solution
Knowledge Check
A wheel of mass 5kg and radius 0.40m is rolling on a road without sliding with angular velocity 10rads−1. The moment of ineria of the wheel about the axis of rotation is 0.65kgm2. The percentage of kinetic energy of rotate in the total kinetic energy of the wheel is.
A22.4%B11.2%C88.8%D44.8%
A uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
View SolutionA sphere of mass m and radius R rolls without sliding on a horizontal surface. It collides with a light spring of stiffness K with a kinetic energy E. If the surface (AB) under the spring is smooth, find the maximum compression of the spring.
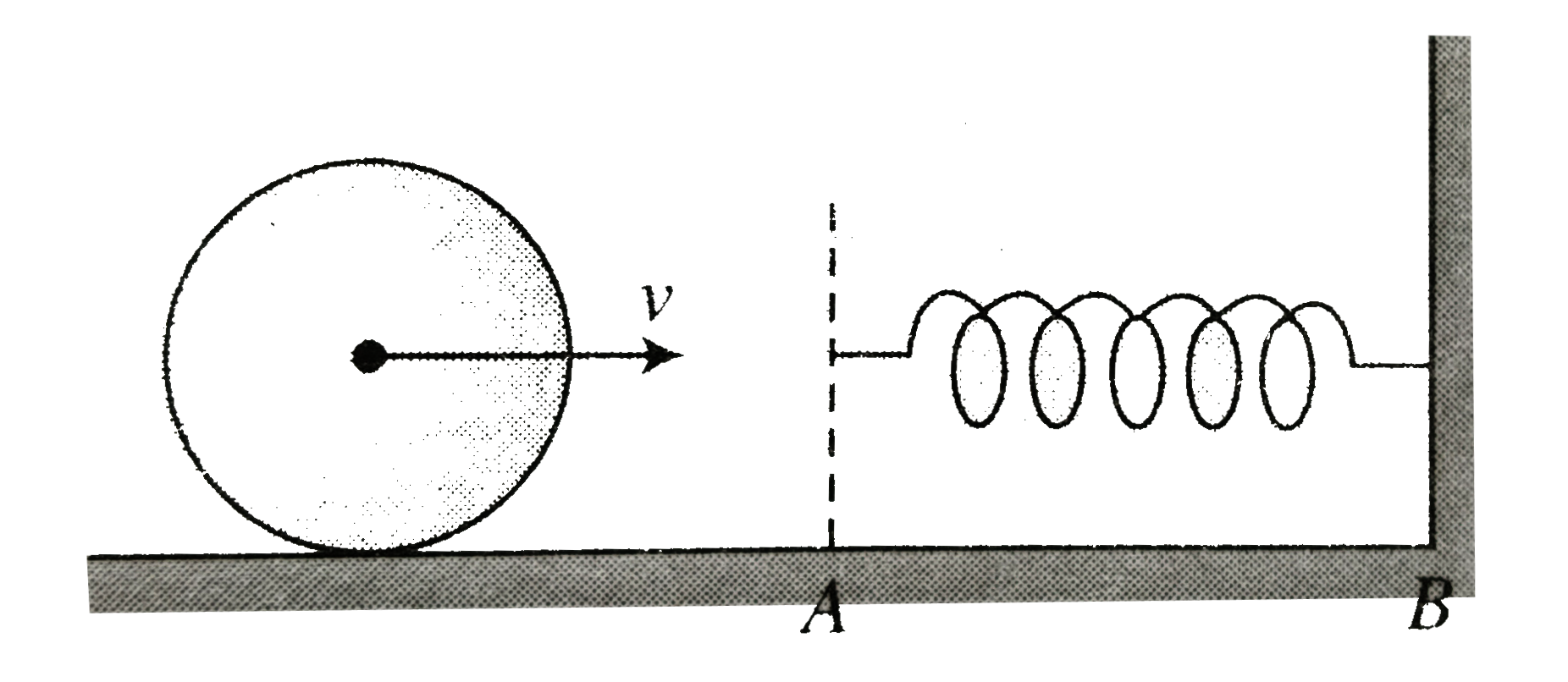
View SolutionA disc of mass 1 kg and radius 0.1 m is rotating with angular velocity 20 rad/s. What is angular velocity (in rad/s) if a mass of 0.5 kg is put on the circumference of the disc ?
View SolutionA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.

View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity ad acceleration vectors of point P is

View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View Solution
