A way pulse is travelling on a string of linear mass density under a load of . Calculate the time taken by the pulse to traverse the string, if its length is .
The correct Answer is:A
To solve the problem, we need to calculate the time taken by a wave pulse to traverse a string of a given length, given its linear mass density and the load applied to it.
1. Identify the Given Values:
- Linear mass density (μ) = 6.4×10−3kg/m
- Load (Tension, T) = 80kgf
- Length of the string (L) = 0.7m
- Acceleration due to gravity (g) = 9.8m/s2
2. Convert Load to Tension:
- The tension in the string can be calculated using the formula:
T=Load×g
- Substituting the values:
T=80kgf×9.8m/s2=80×9.8=784N
3. Calculate the Velocity of the Wave Pulse:
- The velocity (v) of a wave on a string is given by the formula:
v=√Tμ
- Substituting the values for T and μ:
v=√784N6.4×10−3kg/m
4. Perform the Calculation:
- First, calculate the denominator:
μ=6.4×10−3=0.0064kg/m
- Now, calculate:
v=√7840.0064=√122500=350m/s
5. Calculate the Time Taken to Traverse the String:
- The time (t) taken to traverse the length of the string is given by:
t=Lv
- Substituting the values:
t=0.7m350m/s=0.002s=2×10−3s
Final Answer:
The time taken by the pulse to traverse the string is 2×10−3s.
---
- Linear mass density (μ) = 6.4×10−3kg/m
- Load (Tension, T) = 80kgf
- Length of the string (L) = 0.7m
- Acceleration due to gravity (g) = 9.8m/s2
- The tension in the string can be calculated using the formula:
T=Load×g
- Substituting the values:
T=80kgf×9.8m/s2=80×9.8=784N
- The velocity (v) of a wave on a string is given by the formula:
v=√Tμ
- Substituting the values for T and μ:
v=√784N6.4×10−3kg/m
- First, calculate the denominator:
μ=6.4×10−3=0.0064kg/m
- Now, calculate:
v=√7840.0064=√122500=350m/s
- The time (t) taken to traverse the length of the string is given by:
t=Lv
- Substituting the values:
t=0.7m350m/s=0.002s=2×10−3s
The time taken by the pulse to traverse the string is 2×10−3s.
Similar Questions
Figure showa a string of linear mass density 1.0gcm−1onwhichawaveps–eistravell∈g.F∈dthetimetakenbytheps–e∈travell∈gthroughadistanceof50cmonthestr∈g.Takeg=10 ms^-2.
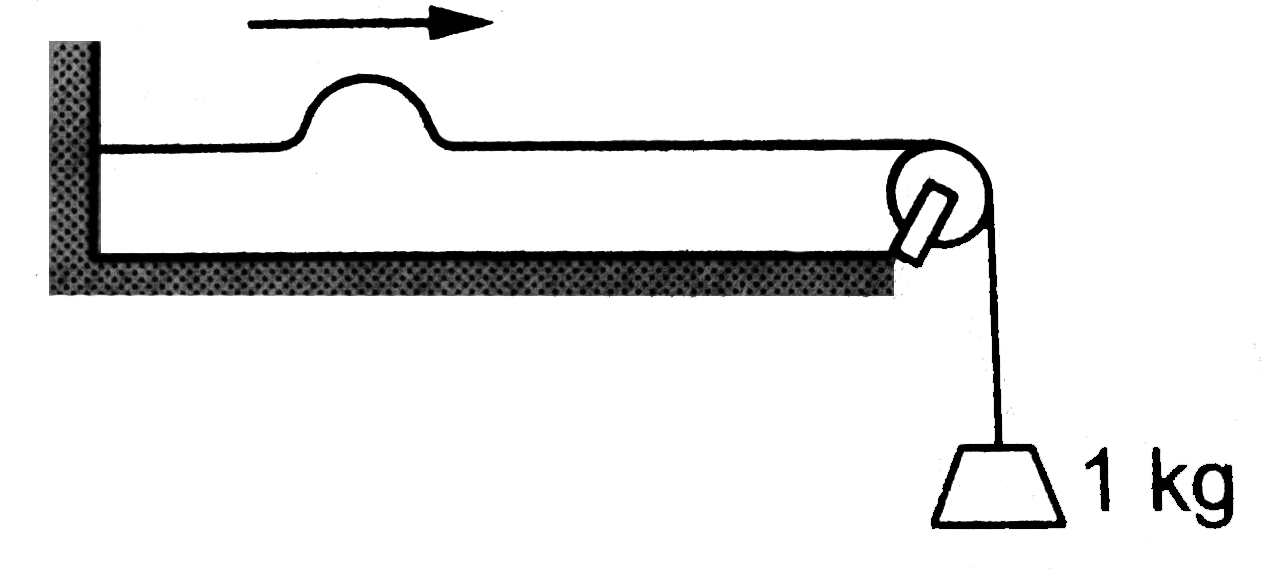
View SolutionA 100 Hz sinusoidal wave is travelling in the positve x - direaction along a string with a linear mass density of 3.5×10−3kgm−1 and a tension of 35 N. At time t =0 ,the point x=0 has zero displacment and the slope of the string is π/20then select the wrong alternative.
View Solution
Knowledge Check
A one meter long string of mass 4.9×10−4 kg is held under a tension of 19.6 N. IF the string vibrates in one segment, then the frequency of vibration will be
A200 HzB100 HzC50 HzD400 Hz
Figure shows different standing wave patterns on a string of linear mass density 4.0×10−2kg/m under a tension of 100 N. The amplitude of antinodes is indicated in each figure. The length of the string is 2.0m.
(i) Obtain the frequencies of the modes shown in figures (a) and (b).
(ii)Write down the transverse displacement y as a function of x and t for each mode. (Take the initial configuration of the wire in each mode to be as shown by the dark lines in the figure).

View SolutionFigure shows a string of linear mass density 1.0gcm−1 on which a wave pulse is travelling. Find the time taken by pulse in travelling through a distance of 50cm on the string. Take g=10ms−2
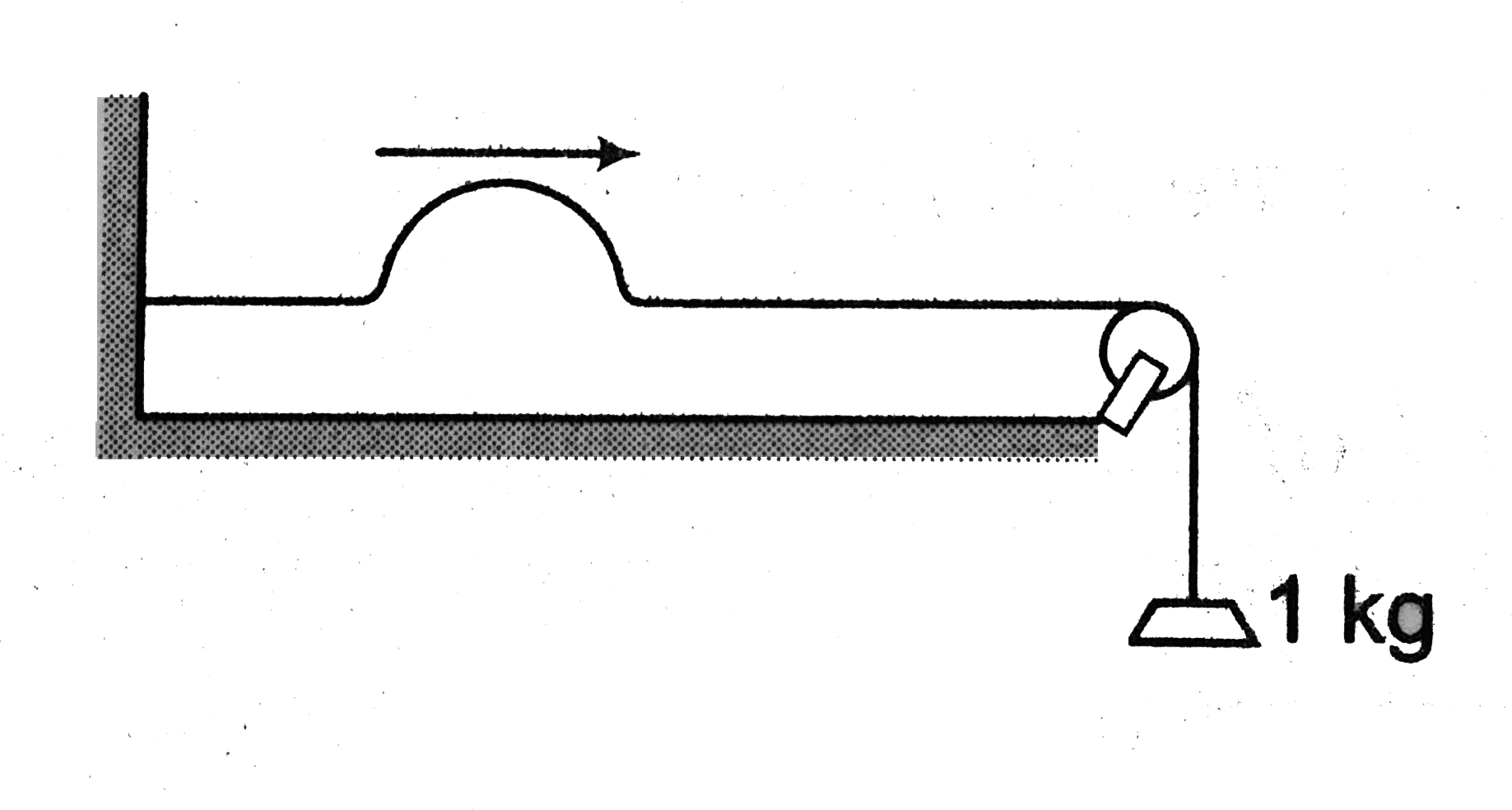
View SolutionA 200Hz wave with amplitude 1mm travels on a long string of linear mass density 6g/m keep under a tension of 60N.
(a) Find the average power transmitted across a given point on the string.
(b) Find the total energy associated with the wave in a 2.0m long portion of the string.
View SolutionA 200Hz wave with amplitude 1mm travels on a long string of linear mass density 6g/m keep under a tension of 60N.
(a) Find the average power transmitted across a given point on the string.
(b) Find the total energy associated with the wave in a 2.0m long portion of the string.
View SolutionThe velocity of transverse wave in string whose linear mass density is 3×10−2kgm stretched by a load of 30 kg is (Take g=10ms2)
View SolutionA piano string having a mass per unit length equal to 5.00×103kg/m is under a tension of 1350N, Find the speed with which a wave travels on this string.
View SolutionThe equation of a wave on a string of linear mass density 0.04kgm−1 is given by
y=0.02(m)sin[2π(t0.04(s)−x0.50(m))].
Then tension in the string is
View Solution