Two tubes A and B are in series. The radius of A is R and that of B is 2R. If water flows through A with velocity v then the velocity of water through B is
v2
v
v4
v8
The correct Answer is:C
To solve the problem, we will use the principle of conservation of mass, which is represented by the equation of continuity for fluid flow.
1. Understand the Setup:
- We have two tubes, A and B, in series.
- The radius of tube A is R.
- The radius of tube B is 2R.
- The velocity of water flowing through tube A is v.
2. Apply the Equation of Continuity:
- The equation of continuity states that the product of the cross-sectional area (A) and the velocity (v) at any two points in a fluid flow must be equal:
A1v1=A2v2
- Here, A1 is the cross-sectional area of tube A, v1 is the velocity in tube A, A2 is the cross-sectional area of tube B, and v2 is the velocity in tube B.
3. Calculate the Areas:
- The cross-sectional area of tube A (radius R):
A1=πR2
- The cross-sectional area of tube B (radius 2R):
A2=π(2R)2=π(4R2)=4πR2
4. Set Up the Equation:
- Substitute the areas and velocities into the equation of continuity:
A1v1=A2v2
πR2⋅v=4πR2⋅v2
5. Simplify the Equation:
- Cancel πR2 from both sides:
v=4v2
6. Solve for v2:
- Rearranging the equation gives:
v2=v4
Final Answer:
The velocity of water flowing through tube B is:
v2=v4
- We have two tubes, A and B, in series.
- The radius of tube A is R.
- The radius of tube B is 2R.
- The velocity of water flowing through tube A is v.
- The equation of continuity states that the product of the cross-sectional area (A) and the velocity (v) at any two points in a fluid flow must be equal:
A1v1=A2v2
- Here, A1 is the cross-sectional area of tube A, v1 is the velocity in tube A, A2 is the cross-sectional area of tube B, and v2 is the velocity in tube B.
- The cross-sectional area of tube A (radius R):
A1=πR2
- The cross-sectional area of tube B (radius 2R):
A2=π(2R)2=π(4R2)=4πR2
- Substitute the areas and velocities into the equation of continuity:
A1v1=A2v2
πR2⋅v=4πR2⋅v2
- Cancel πR2 from both sides:
v=4v2
- Rearranging the equation gives:
v2=v4
The velocity of water flowing through tube B is:
v2=v4
Similar Questions
A liquid flows through two capillary tubes A and B connected in series. The length and radius of B are twice that of A. What is the ratio of the pressure difference across A to that across B ?
View SolutionWater is flowing through a horizontal tube of non-uniform cross-section. At a place, the radius of the tube is 1.0cm and the velocity of water is 2m/s. What will be the velocity of water where the radius of the pipe is 2.0cm?
View Solution
Knowledge Check
Two planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity VA/VB is
A2B√2C1/√2D1/2An incompressible fluid flows steadily through a cylinder pipe which has radius 2 R at point A and radius R at point B further along the flow direction. IF the velocity at point A is v, its velocity at a point B will be
A2 vBvCv/2D4v
The cross-sectionss of a pipe at two points A and B are in the ratio 1.4. If the speed of water flowing through the pipe at point A is v, its speed at point B is
View SolutionA current .I. flows through a metallic wire of radius .r. and the free electrons in it drift with a velocity vd. Calculate the drift velocity of the free electrons through the wire of the same material, having double the radius, when same current flows through it.
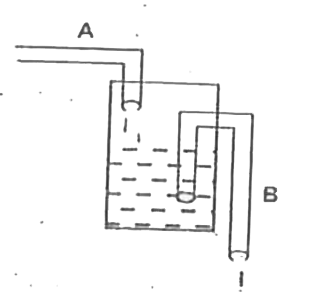
View SolutionThe velocity of the water flowing from the inlet pipe is less than the velocity of water flowing out from the spin pipe B. Then
View SolutionTwo capillary of length L and 2L and of radius R and 2R are connected in series. The net rate of flow of fluid through them will be (given rate to the flow through single capillary,
(X=πPR48ηL)
View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 2I is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionA conical section of a pipe is shown in figure through which water is flowing. Let A be the area of crosss-section, r be the radius of cross-section, P be the pressure at a point difference and v be the velocity of water.

Match the column-I with column-II containing values of ratio of quantities given in Column-I
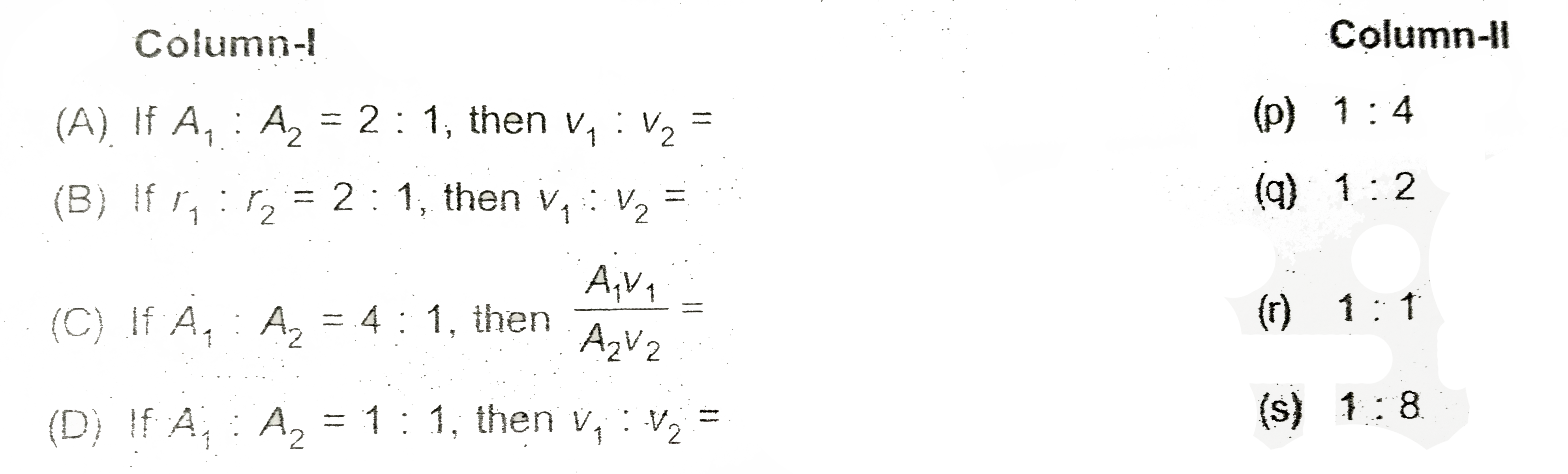
View Solution
