Two capillary of length L and 2L and of radius R and 2R are connected in series. The net rate of flow of fluid through them will be (given rate to the flow through single capillary,
(X=πPR48ηL)
89X
98X
57X
75X
The correct Answer is:A
To solve the problem, we need to determine the net rate of flow of fluid through two capillaries connected in series. We are given the formula for the flow rate through a single capillary:
X=πPR48ηL
where:
- P is the pressure difference,
- R is the radius of the capillary,
- η is the viscosity of the fluid,
- L is the length of the capillary.
1. Identify the Capillaries:
- The first capillary has a length L and radius R.
- The second capillary has a length 2L and radius 2R.
2. Calculate the Resistance of Each Capillary:
- The resistance R1 of the first capillary (length L, radius R) is given by:
R1=8ηLπR4
- The resistance R2 of the second capillary (length 2L, radius 2R) is given by:
R2=8η(2L)π(2R)4=8η(2L)π(16R4)=ηLπR4
3. Calculate the Total Resistance in Series:
- When two resistances are in series, the total resistance Req is the sum of the individual resistances:
Req=R1+R2=8ηLπR4+ηLπR4=9ηLπR4
4. Determine the Net Flow Rate:
- The net flow rate Qnet through the combined capillaries can be expressed using the pressure and the equivalent resistance:
Qnet=PReq
- Substituting Req:
Qnet=P⋅πR49ηL
5. Relate to Given Flow Rate X:
- We know from the given formula that:
X=πPR48ηL
- Therefore, we can express Qnet in terms of X:
Qnet=89X
Final Answer:
The net rate of flow of fluid through the two capillaries connected in series is:
Qnet=89X
- P is the pressure difference,
- R is the radius of the capillary,
- η is the viscosity of the fluid,
- L is the length of the capillary.
- The first capillary has a length L and radius R.
- The second capillary has a length 2L and radius 2R.
- The resistance R1 of the first capillary (length L, radius R) is given by:
R1=8ηLπR4
- The resistance R2 of the second capillary (length 2L, radius 2R) is given by:
R2=8η(2L)π(2R)4=8η(2L)π(16R4)=ηLπR4
- When two resistances are in series, the total resistance Req is the sum of the individual resistances:
Req=R1+R2=8ηLπR4+ηLπR4=9ηLπR4
- The net flow rate Qnet through the combined capillaries can be expressed using the pressure and the equivalent resistance:
Qnet=PReq
- Substituting Req:
Qnet=P⋅πR49ηL
- We know from the given formula that:
X=πPR48ηL
- Therefore, we can express Qnet in terms of X:
Qnet=89X
The net rate of flow of fluid through the two capillaries connected in series is:
Qnet=89X
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question19videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns6videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.410videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
Two capillary tubes of lengths in the ratio 2:1 and radii in the ratio 1:2 are connected in series. Assume the flow of the liquid through the tube is steady. Then, the ratio of pressure difference across the tubes is
View SolutionA capillary tube of length 5 cm and diameter 1 mm is connected to a tank horizontally. The rate of flow of water is 10 ce per minute. Calculate the rate of flow of water through another capillary tube of diameter 2 mm and length 50 cm is connected in series with the first capillary?
View Solution
Knowledge Check
- Question 1 - Select One
Two copper wire of length l and 2l have radii, r and 2r respectively. What si the ratio of their specific resistance.?
A1:2B2:1C1:1D1:3 - Question 2 - Select One
Two capillaries of same length and radii in the ratio 1:2 are connected in series. A liquid flows through them in streamlined condition. If the pressure across the two extreme ends of the combination is 1 m of water, the pressure difference across first capillary is
A9.4 mB4.9 mC0.49 mD0.94 m
If Q is the rate of flow of liquid through a capillary tube of length l and radius r at constant pressure P, then the rate of flow of liquid through a capillary tube when radius is reduced to one third and length of tube is doubled
View SolutionAn inducatane L and a resistance R are connected in series with a battery of emf epsilon. Find the maximum rate at which the energy is stored in the magnetic field.
View SolutionTwo tubes A and B are in series. The radius of A is R and that of B is 2R. If water flows through A with velocity v then the velocity of water through B is
View SolutionFigure below shows a capacitor C, an inductor L and a resistor R, connected in series to an a.c. supply of 220 V.
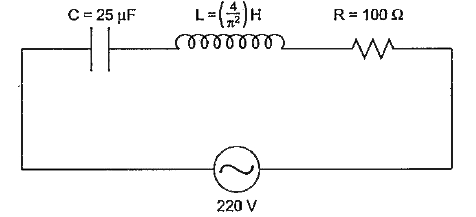
Current flowing through the circuit.View SolutionThe given circuit has two ideal diodes connected as show in the figure. The current flowing through the resistance R1 will be
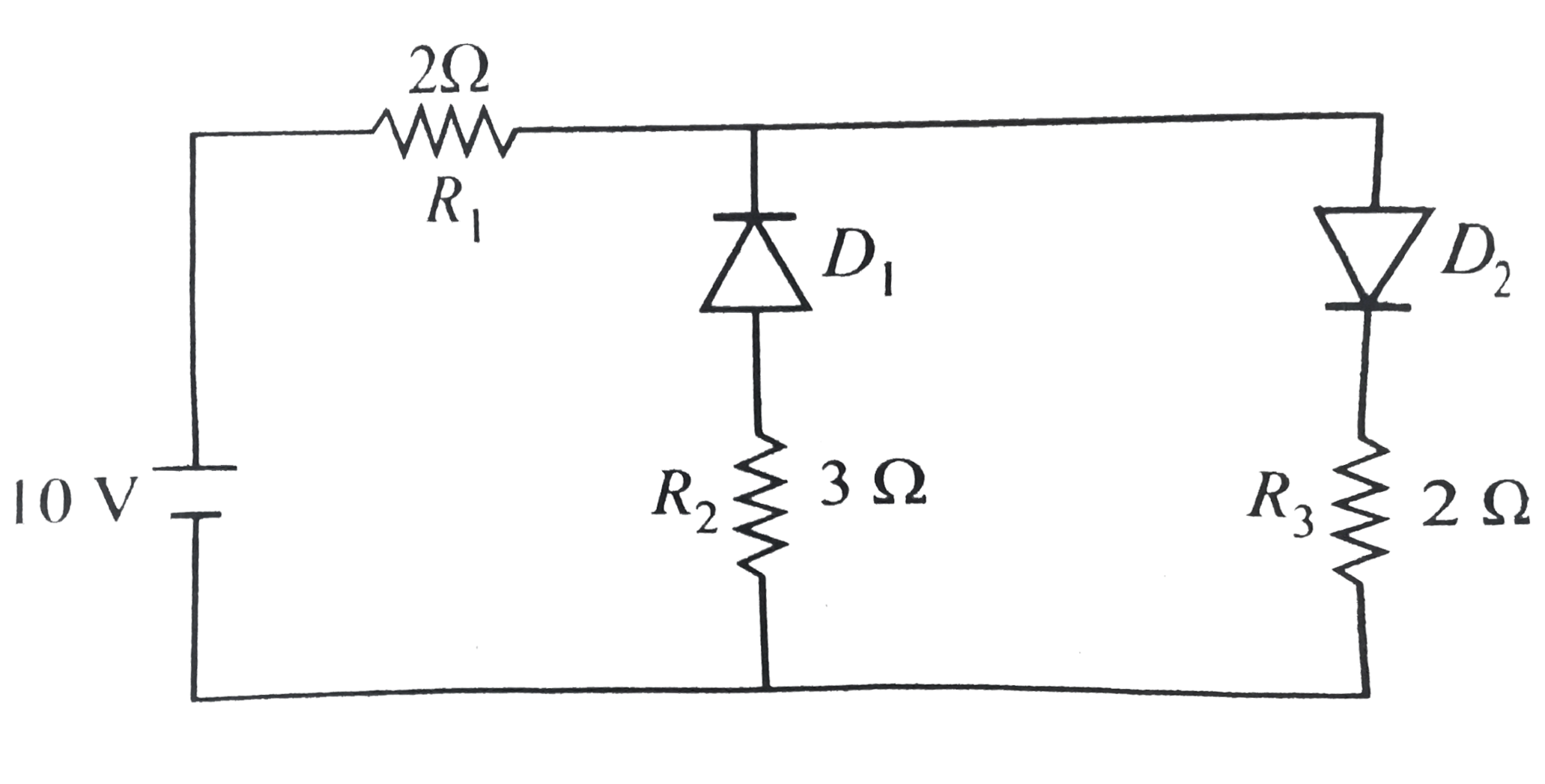 View Solution
View SolutionAn inductor L and a resistor R are connected in series to a battery, through a key/switch. Show graphically, how current decreases with time when the key/switch is opened.
View Solution

