A circuit has a self inductance of 1H and carries a current of 2A. To prevent sparking when the circuit is switched off, a capacitor which can withstand 400V is used. The least capacitance of the capacitor connected across the switch must be equal to
The correct Answer is:B
To solve the problem, we need to determine the least capacitance of the capacitor that can prevent sparking when the circuit is switched off. Here's the step-by-step solution:
Step 1: Identify the energy stored in the inductor
The energy (E) stored in an inductor can be calculated using the formula:
E=12LI2
where:
- L is the self-inductance (1 H),
- I is the current (2 A).
Step 2: Calculate the energy stored in the inductor
Substituting the values into the formula:
E=12×1×(2)2=12×1×4=2 Joules
Step 3: Identify the energy stored in the capacitor
The energy stored in a capacitor can be calculated using the formula:
E=12CV2
where:
- C is the capacitance,
- V is the voltage (400 V).
Step 4: Set the energy of the inductor equal to the energy of the capacitor
To prevent sparking, the energy stored in the capacitor must equal the energy released by the inductor:
12CV2=2
Step 5: Solve for capacitance C
Rearranging the equation to solve for C:
C=2×2V2
Substituting V=400 V:
C=2×2(400)2=4160000=140000 Farads
Step 6: Convert Farads to microfarads
To convert Farads to microfarads, we multiply by 106:
C=140000×106=25 microfarads
Final Answer
The least capacitance of the capacitor connected across the switch must be equal to:
25 microfarads
---
The energy (E) stored in an inductor can be calculated using the formula:
E=12LI2
where:
- L is the self-inductance (1 H),
- I is the current (2 A).
Substituting the values into the formula:
E=12×1×(2)2=12×1×4=2 Joules
The energy stored in a capacitor can be calculated using the formula:
E=12CV2
where:
- C is the capacitance,
- V is the voltage (400 V).
To prevent sparking, the energy stored in the capacitor must equal the energy released by the inductor:
12CV2=2
Rearranging the equation to solve for C:
C=2×2V2
Substituting V=400 V:
C=2×2(400)2=4160000=140000 Farads
To convert Farads to microfarads, we multiply by 106:
C=140000×106=25 microfarads
The least capacitance of the capacitor connected across the switch must be equal to:
25 microfarads
Similar Questions
An inductance of 2H carries a current of 2A. To prevent sparking when the circuit is broken a capacitor of 4μF is connected across the inductance. The voltage rating of the capacitor is of the order of
View SolutionFind out current in the circuit and charge on capacitor which is initially uncharged in the following situations.
(a) Just after the switch is closed.
(b) After a long time when switch was closed.
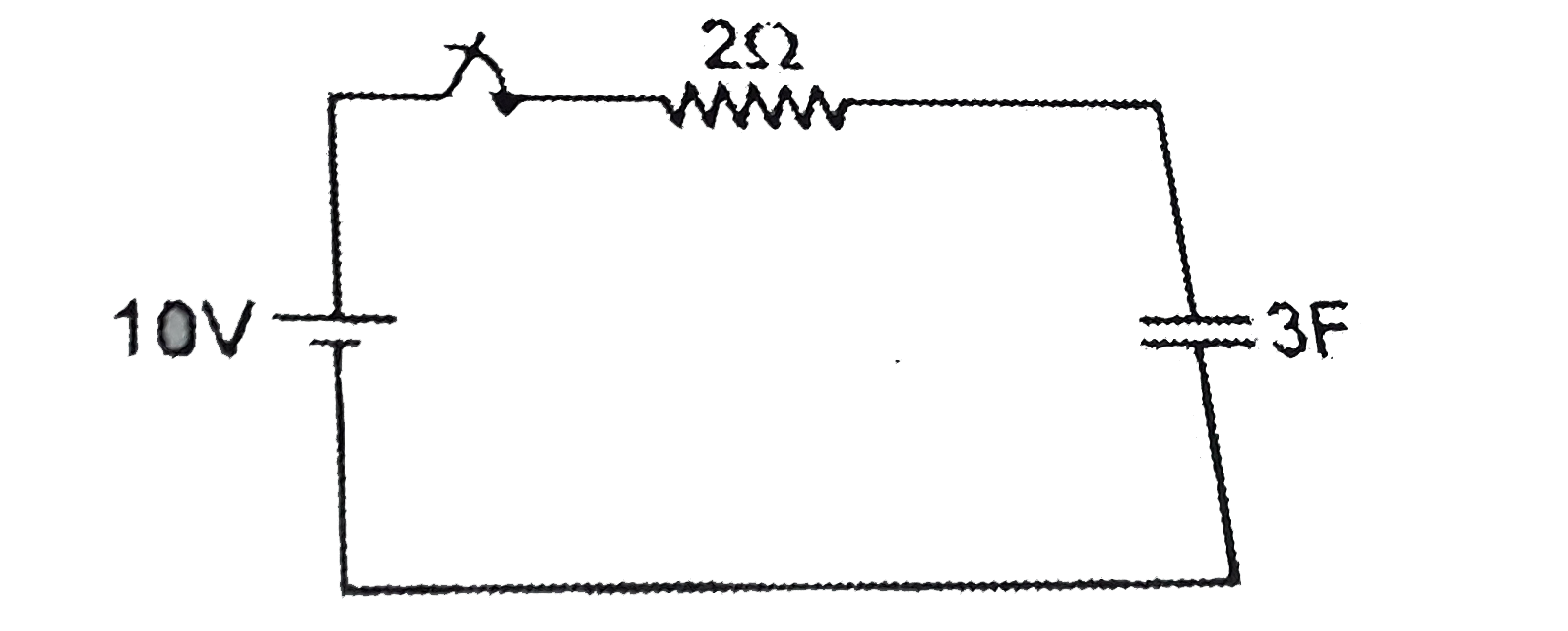 View Solution
View SolutionCondsider
 .
.
In the circuit shown is the switch can be shifted to positions 1 and 2 The charge on capacitor C1 when the switch is at position 1 is.View SolutionTwo capacitors of capacitance 2μFand5μF are charged to a potential difference 100V and 50 V respectively and connected such that the positive plate of one capacitor is connected to the negative plate of the other capacitor after the switch is closed, the initial current in the circuit is 50 mA. the total resistance of the connecting wires is (in Ohm):
View SolutionAn inductor coil carries a steady state current of 2.0 A when connected across an ideal battery of emf 4.0 V. if its inductance is 1.0 H, find the time constant of the circuit.
View SolutionA capacitor of capacitance 25μF is charged to 300V. It is then connected across a 10mH inductor. The resistance in the circuit is negligible.
a. Find the frequency of oscillation of the circuit.
b. Find the potential difference across capacitor and magnitude of circuit current 1.2ms after the inductor and capacitor are connected.
c. Find the magnetic energy and electric energy at t=0 and t=1.2ms.View SolutionAn RC circuit is made using five identical capacitors, each of which can withstand a maximum voltage of 2 volts. The maximum voltage which can be safely applied across points A and B is
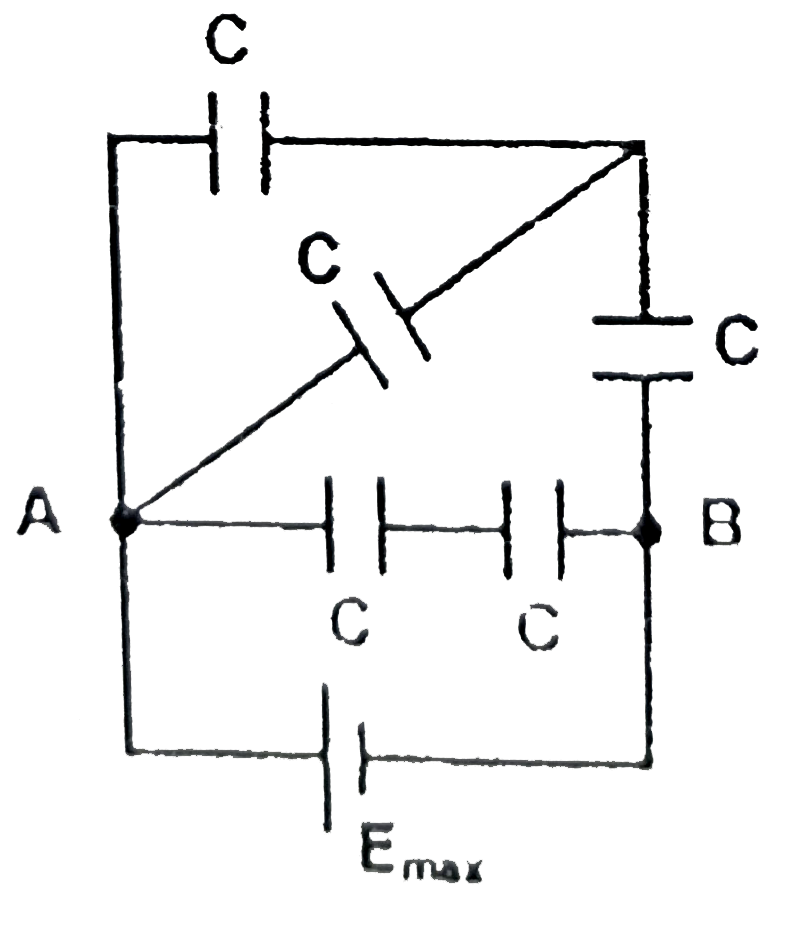 View Solution
View SolutionA current of 4A flows in a coil when connected to a 12VDC source. If the same coil is connected to a 12V,50rad/sAC source, a current of 2.4A flows in the circuit. Determine the inductance of the coil. Also, find the power developed in the circuit if a2500μF capacitor is connected in series with the coil.
View SolutionA current of 4A flows in a coil when connected to a 12VDC source. If the same coil is connected to a 12V,50rad/sAC source, a current of 2.4A flows in the circuit. Determine the inductance of the coil. Also, find the power developed in the circuit if a2500μF capacitor is connected in series with the coil.
View SolutionA current of 4A flows in a coil when connected to a 12VDC source. If the same coil is connected to a 12V,50rad/sAC source, a current of 2.4A flows in the circuit. Determine the inductance of the coil. Also, find the power developed in the circuit if a2500μF capacitor is connected in series with the coil.
View Solution

