The temperature of a ideal gas is increased for 100 k to 400k. If at 100 K the root mea square velocity of the gas molecules is v, at 400K it becomes
2V
4V
0.5V
V
The correct Answer is:A
To solve the problem, we need to find the root mean square (RMS) velocity of an ideal gas when its temperature is increased from 100 K to 400 K.
1. Understand the relationship between RMS velocity and temperature:
The root mean square velocity (v_rms) of gas molecules is given by the formula:
vrms=√3RTM
where R is the universal gas constant, T is the absolute temperature, and M is the molar mass of the gas.
2. Identify the initial and final temperatures:
- Initial temperature, T1=100K
- Final temperature, T2=400K
3. Express the RMS velocities at the two temperatures:
Let v1 be the RMS velocity at T1 and v2 be the RMS velocity at T2.
From the formula, we have:
v1=√3RT1Mandv2=√3RT2M
4. Set up the ratio of the RMS velocities:
Taking the ratio of v1 and v2:
v1v2=√3RT1M√3RT2M=√T1T2
5. Substituting the values of T1 and T2:
v1v2=√100400=√14=12
6. Finding v2:
From the ratio, we can express v2 in terms of v1:
v2=2v1
Since v1=V, we have:
v2=2V
7. Conclusion:
Therefore, the root mean square velocity at 400 K is 2V.
Final Answer:
The root mean square velocity at 400 K becomes 2V.
The root mean square velocity (v_rms) of gas molecules is given by the formula:
vrms=√3RTM
where R is the universal gas constant, T is the absolute temperature, and M is the molar mass of the gas.
- Initial temperature, T1=100K
- Final temperature, T2=400K
Let v1 be the RMS velocity at T1 and v2 be the RMS velocity at T2.
From the formula, we have:
v1=√3RT1Mandv2=√3RT2M
Taking the ratio of v1 and v2:
v1v2=√3RT1M√3RT2M=√T1T2
v1v2=√100400=√14=12
From the ratio, we can express v2 in terms of v1:
v2=2v1
Since v1=V, we have:
v2=2V
Therefore, the root mean square velocity at 400 K is 2V.
The root mean square velocity at 400 K becomes 2V.
Similar Questions
Knowledge Check
The temperature of an ideal gas is increased from 120 K to 480 K. If at 120 K the root mean square velocity of the gas molecules is v, at 480 K it becomes
A4vrmsB2vrmsC2vrms2Dvrms4
The temperature at which the root mean square velocity of the gas molecules would becomes twice of its value at 0∘C is
View SolutionThe temperature of 20 litres of nitrogen was increased from 100 K to 300 K at a constant pressure. Change in volume will be
View SolutionTemperature of 4 moles of gas increases from 300 K to 500 K find Cv if ΔU=5000J.
View SolutionThe temperature of air in a 900m long tunnel varies linearly form 100K at one end to 900K at other end. If the speed of sound in air at 400K is 360m/s then time taken by sound to cross the tunnel is K second. Find 2K ?
View SolutionA mass M = 15 g of nitrogen is enclosed in a vessel at temperature T = 300 K. What amount of heat has to be transferred to the gas to increase the root-mean-square velocity of molecules 2 times ?
View SolutionA mass M = 15 g of nitrogen is enclosed in a vessel at temperature T = 300 K. What amount of heat has to be transferred to the gas to increase the root-mean-square velocity of molecules 2 times ?
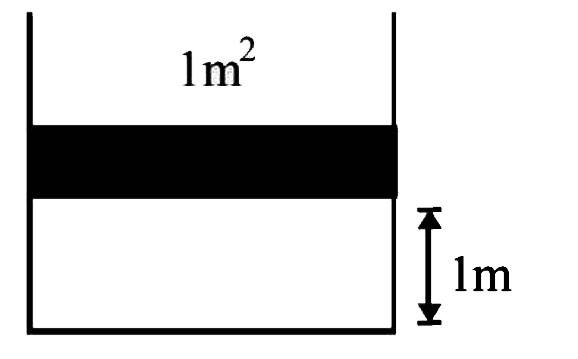
View SolutionA diatomic gas is enclosed in a vessel fitted with massless movable piston. Area of cross section of vessel is 1m2. Initial height of the piston is 1m (see the figure). The initial temperature of the gas is 300K. The temperature of the gas is increased to 400K, keeping pressure constant, calculate the new height of the piston. The piston is brought to its initial position with no heat exchange. Calculate the final temperature of the gas. You can leave answer in fraction.
View Solution