Line PQ is parallel to y - axis and moment of inertia of a rigid body about PQ line is given by I=2x2−12x+27, where x is in meter and I is in kg m3. The minimum value of I is :
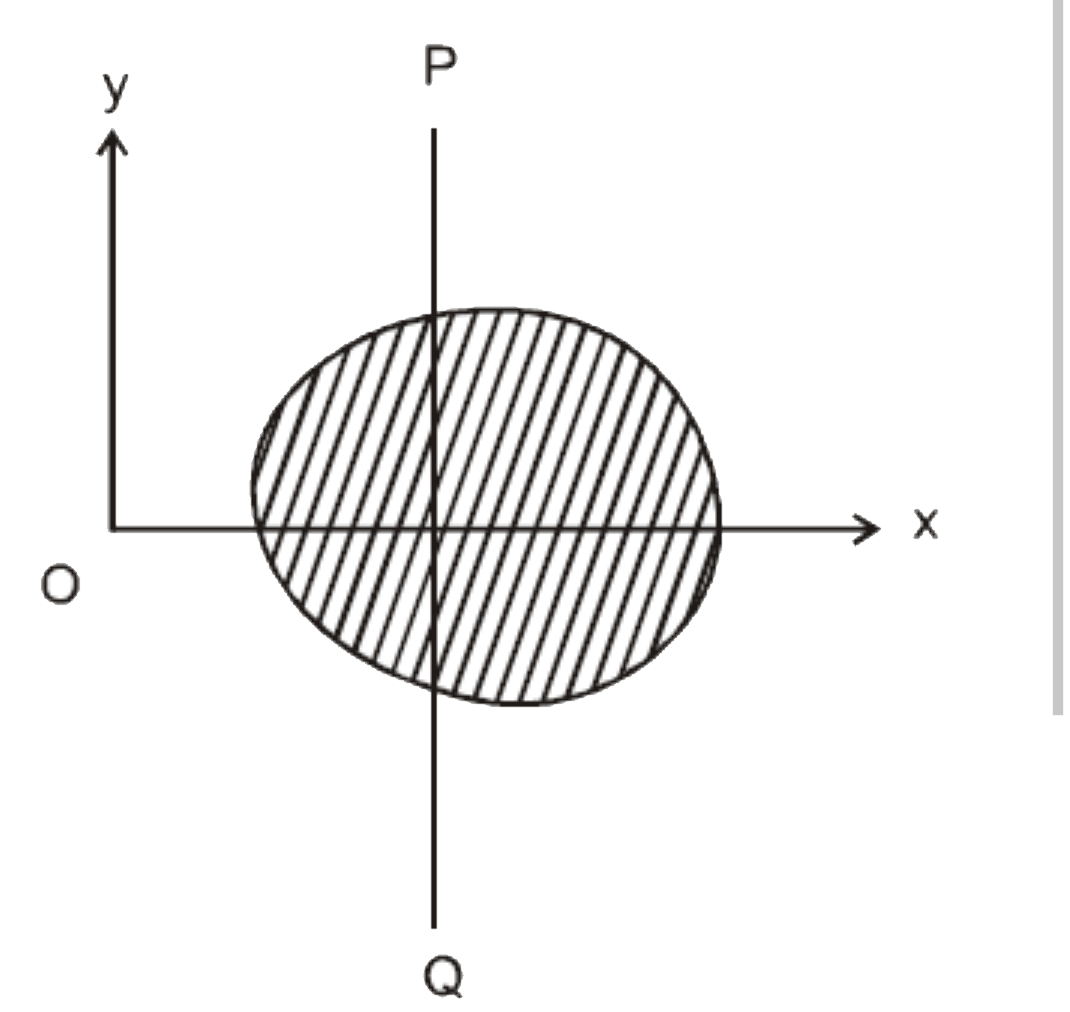
27 kg m2
11 kg m2
17 kg m2
9 kg m2
The correct Answer is:D
Step by step video & image solution for Line PQ is parallel to y - axis and moment of inertia of a rigid body about PQ line is given by I=2x^(2)-12x+27, where x is in meter and I is in "kg m"^(3). The minimum value of I is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Assertion: Moment of inertia of a rigid body about any axis passing through its centre of mass is minimum
Reason: From theorem of parallel axis
I=Icm+Mr2
View SolutionMoment of inertia I of a solid sphere about an axis parallel to a diameter and at a distance x from it varies as:
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View SolutionThe axis X and Z in the plane of a disc are mutually perpendicular and Y-axis is perpendicular to the plane of the disc. If the moment of inertia of the body about X and Y axes is respectively 30 kg m2 and 40 kg m2 then M.I. about Z-axis in kg m2 will be:
View SolutionFind the values of x and y , if 2 x + 3yi = 2+ 12i , where x,y∈R
View SolutionA rigid body can be hinged about any point on the x-axis. When it is hinged such that the hinge is at x, the moment of interia is given by
I=2x2−12x+27
The x-coordinate of centre of mass is.
View SolutionFind the equation of the following lines :
(i) parallel to X-axis and 2 units above it.
(ii) parallel to X-axis and 3 units below it.
(iii) parallel to Y-axis and 6 units left of it.
(i) parallel to Y-axis and 4 units right of it.
View SolutionIf line 3x−ay−1=0 is parallel to the line (a+2)x−y+3=0 then find the value of a.
View SolutionStatement-1: if moment of inertia of a rigid body is equal about two axis, then both the axis must be parallel.
Statement-2 from parallel axis theorem I=Icm+md2, where all terms have usual meaning.
View SolutionA uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
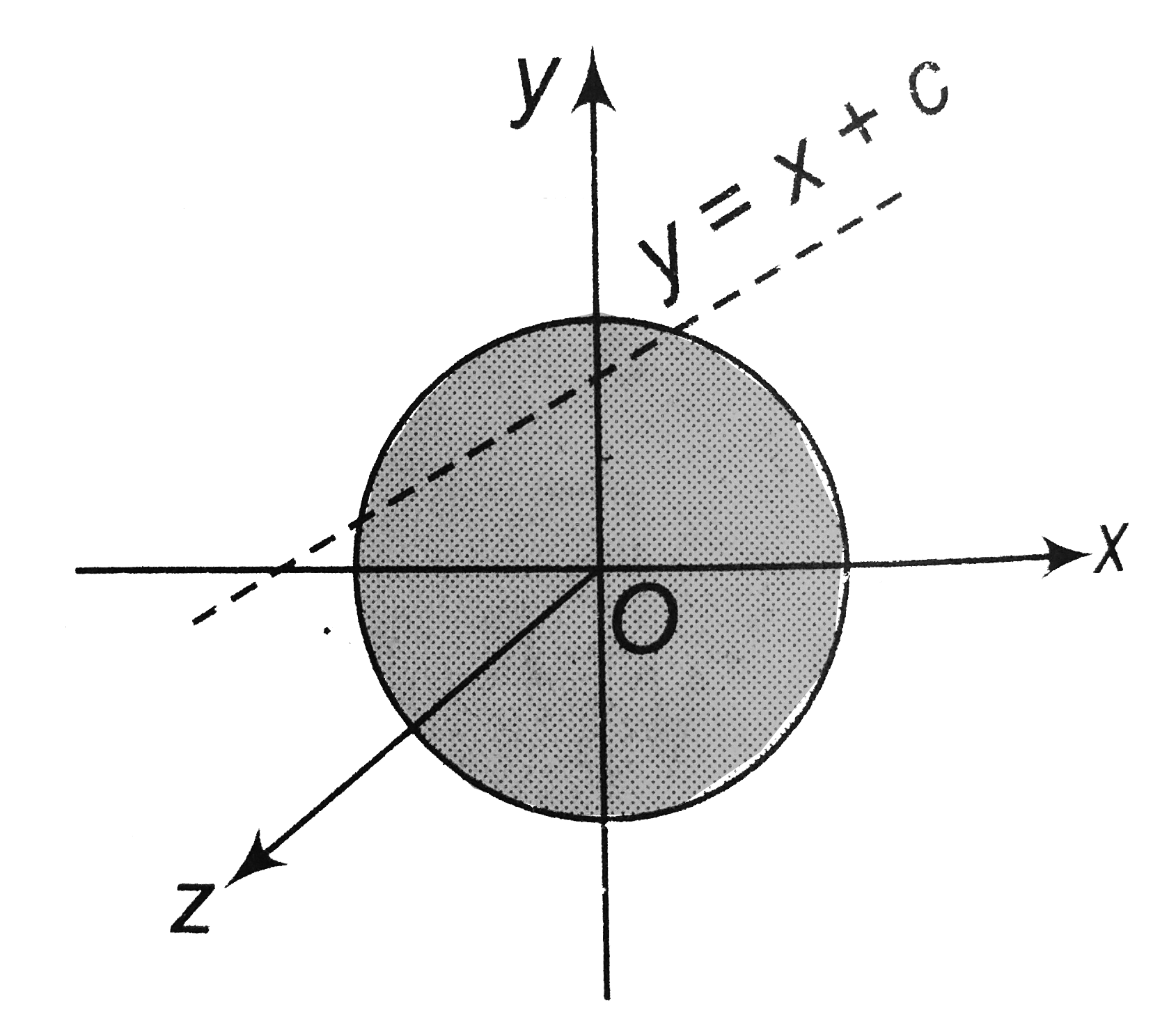 .
.
View Solution
