An oil drop carrying a charge q has a mass m kg. it is falling freely in air with terminal speed v. the electric field required to make, the drop move upwards with the same speed is
The correct Answer is:B
To solve the problem, we need to determine the electric field required to make an oil drop move upwards with the same terminal speed v that it has while falling freely under the influence of gravity and air resistance.
1. Identify the Forces Acting on the Oil Drop:
- When the oil drop is falling freely, it experiences two forces:
- The gravitational force acting downwards: Fg=mg
- The viscous drag force acting upwards: Fd=6πηrv (according to Stokes' law)
- At terminal velocity, these forces balance out:
mg=6πηrv(1)
2. Set Up the Forces When the Drop Moves Upwards:
- When an electric field E is applied, it exerts an upward force on the charged drop:
- The electric force: Fe=qE
- The forces acting on the drop moving upwards are:
- The upward electric force: Fe=qE
- The downward gravitational force: Fg=mg
- The upward viscous drag force: Fd=6πηrv
3. Balance the Forces for Upward Motion:
- For the drop to move upwards with the same speed v, the net force must be zero:
qE=mg+6πηrv(2)
4. Substitute Equation (1) into Equation (2):
- From Equation (1), we know that mg=6πηrv. Therefore, we can substitute mg in Equation (2):
qE=mg+mg
- This simplifies to:
qE=2mg
5. Solve for the Electric Field E:
- Rearranging the equation gives:
E=2mgq
Final Answer:
The electric field required to make the drop move upwards with the same speed v is:
E=2mgq
- When the oil drop is falling freely, it experiences two forces:
- The gravitational force acting downwards: Fg=mg
- The viscous drag force acting upwards: Fd=6πηrv (according to Stokes' law)
- At terminal velocity, these forces balance out:
mg=6πηrv(1)
- When an electric field E is applied, it exerts an upward force on the charged drop:
- The electric force: Fe=qE
- The forces acting on the drop moving upwards are:
- The upward electric force: Fe=qE
- The downward gravitational force: Fg=mg
- The upward viscous drag force: Fd=6πηrv
- For the drop to move upwards with the same speed v, the net force must be zero:
qE=mg+6πηrv(2)
- From Equation (1), we know that mg=6πηrv. Therefore, we can substitute mg in Equation (2):
qE=mg+mg
- This simplifies to:
qE=2mg
- Rearranging the equation gives:
E=2mgq
The electric field required to make the drop move upwards with the same speed v is:
E=2mgq
Similar Questions
An oil drop, carrying six electronic charges and having a mass of 1.6×10−12g, falls with some terminal velocity in a medium. What magnitude of vertical electric field is required to make the drop move upward with the same speed as it was formerly moving down ward with ? Ignore buoyancy.
View SolutionAn oil drop having a charge q and apparent weight W falls with a terminal speed v in absence of electric field . When electric field is switched on it starts moving up with terminal speed v. The strength of electric field is
View Solution
Knowledge Check
A tiny spherical oil drop carrying a net charge q is balanced in still air with a vertical uniform electric field of strength 81π7×105Vm−1. When the field is switched off, the drop is observed to fall with terminal velocity 2×10−3ms−1. Given g=9.8ms−2, viscoisty of the air =1.8×10−5Nsm−2 and the denisty of oil =900kgm−3, the magnitude of q is
A1.6×10−19 CB3.2×10−19 CC4.8×10−19 CD8.0×10−19 C
The terminal speed v of a rain water drop in air is :
View SolutionAn oil drop has a charge −9.6×10−19C and mass 1.6×10−15 gm. When allowed to fall, due to air resistance force it attains a constant velocity. Then if a uniform electric field is to be applied vertically to make the oil drop ascend up with the same constant speed, which of the following are correct. (g=10ms−2) (Assume that the magnitude of resistance force is same in both the cases)
View SolutionA charged particle of mass m is moving with a speed u in a circle of radius r. If the magnetic field induction at the centre is B, the charge on the particle is
View SolutionTwo drops of same radius are falling through air with steady speed v. If the two drops coalesce, what would be the terminal speed –
View SolutionA particle of mass m and charge −q is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement. Neglect gravity
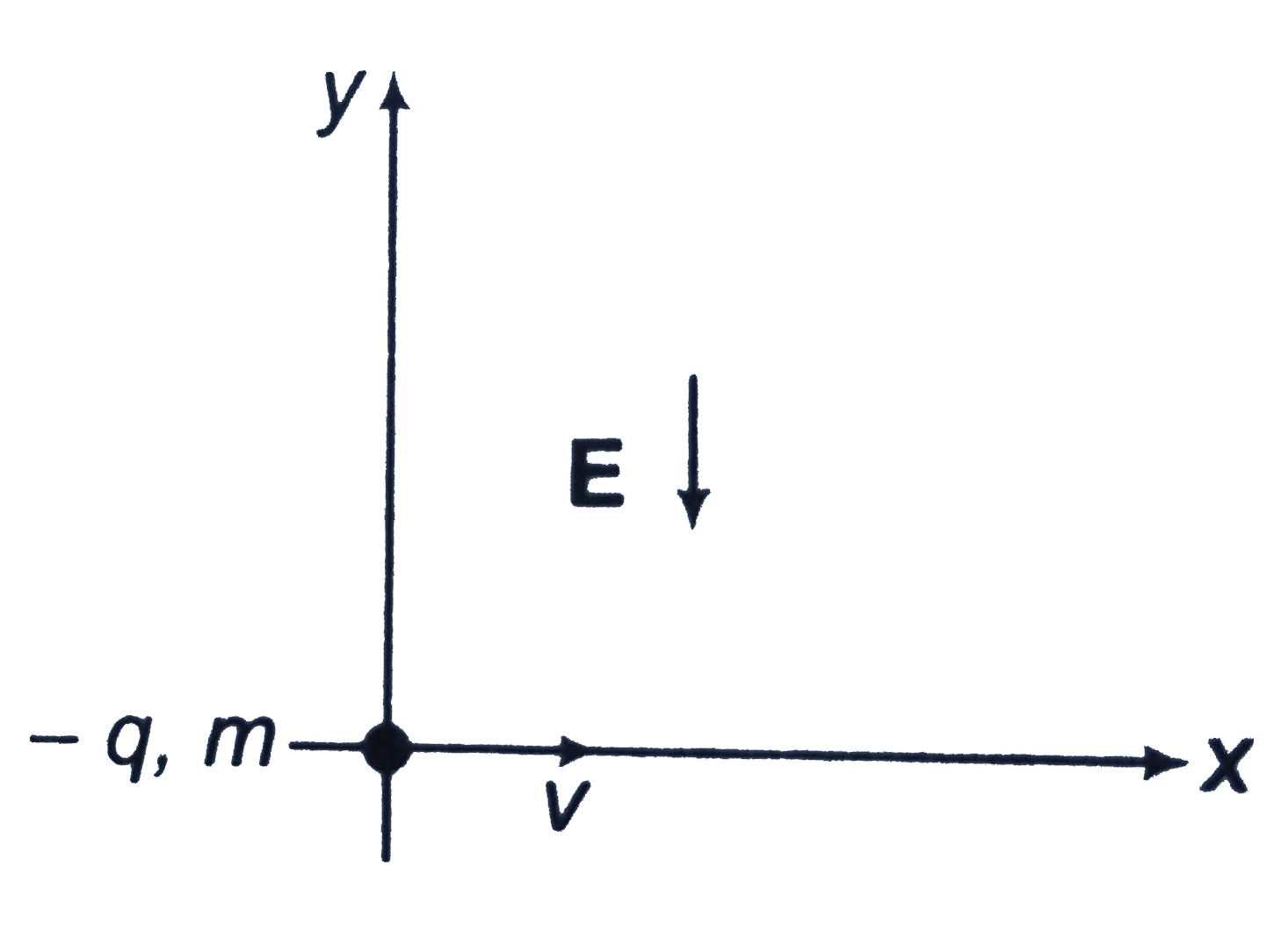
View SolutionA particle of mass m and charge −q is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement. Neglect gravity

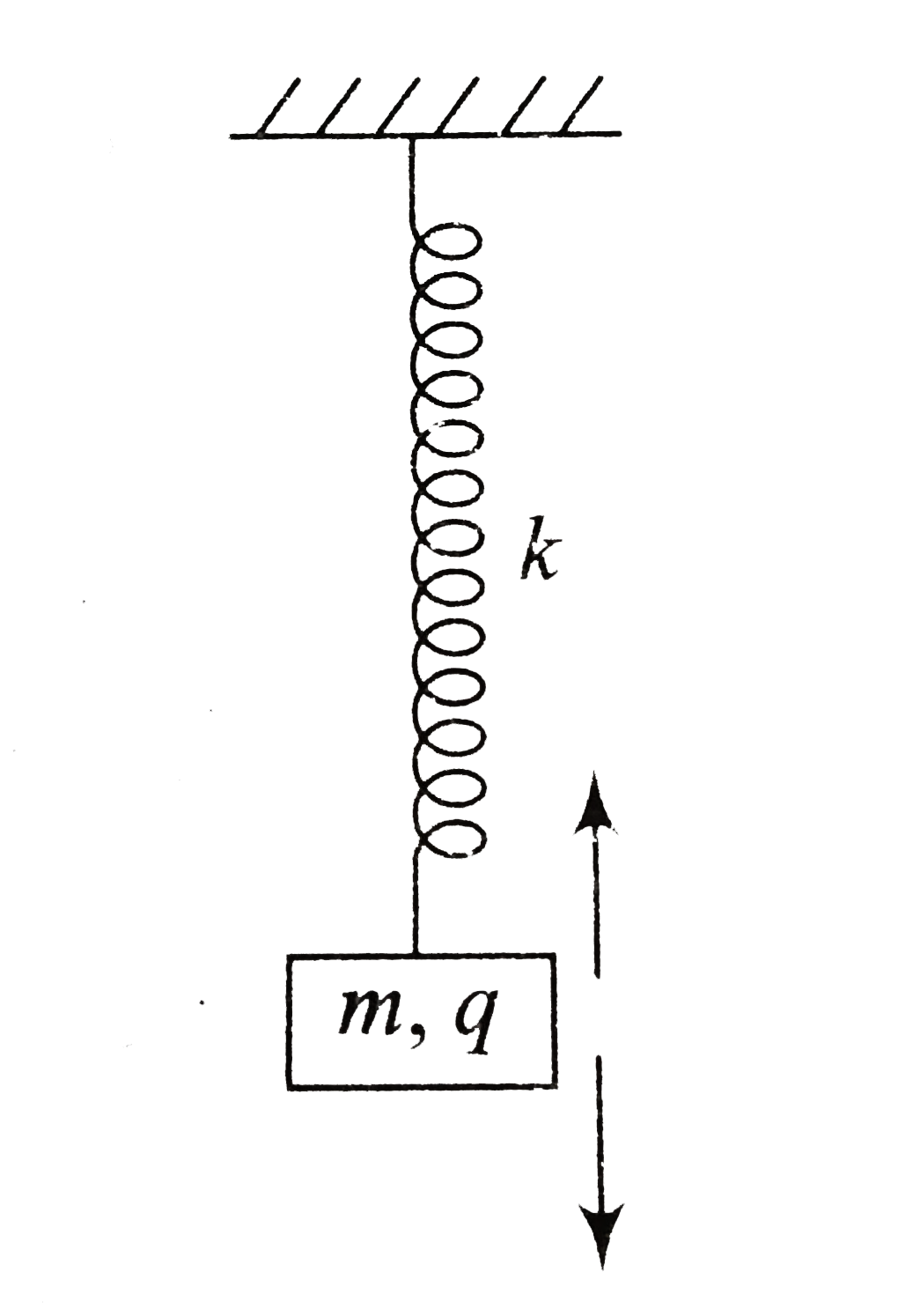
View SolutionThe following figure shows a block of mass m suspended from a fixed point by means of a vertical spring. The block is oscillatting simple harmonically and carries a charge q. There also exists a uniform electric field in the region. Consider four different cases. The electric field is zero in case 1, mg/q downward in case 2, mg/q upward in case 3, and 2mg/q downward in case 4. The speed at mean position is same in all cases. Select the correct alternative (s).
View Solution
