White light reflected at normal incidence from a soap film has minima at 6500Å and maxima at 7500Å in the visible region without minimum in between. If μ is 53 for the thin film, thickness of the film is
7.40×10−7m
9.75×10−5mm
9.40×10−7cm
9.75×10−4mm
The correct Answer is:A
To find the thickness of the soap film, we will use the conditions for constructive and destructive interference in thin films. Here’s the step-by-step solution:
Step 1: Understand the Conditions for Minima and Maxima
For a thin film, the conditions for maxima and minima are given by:
- For maxima: 2μt=(n+12)λmax
- For minima: 2μt=nλmin
Where:
- μ is the refractive index of the film,
- t is the thickness of the film,
- n is an integer (order of interference),
- λmax and λmin are the wavelengths of light corresponding to maxima and minima respectively.
Step 2: Set Up the Equations
From the problem:
- λmin=6500Å=6500×10−10m
- λmax=7500Å=7500×10−10m
- μ=53
We can write the equations for maxima and minima:
1. 2μt=(n+12)λmax
2. 2μt=nλmin
Step 3: Equate the Two Expressions
Since both expressions are equal to 2μt, we can set them equal to each other:
(n+12)λmax=nλmin
Step 4: Substitute the Values
Substituting the values of λmax and λmin:
(n+12)(7500×10−10)=n(6500×10−10)
Step 5: Simplify the Equation
Cancelling 10−10 from both sides:
(n+12)(7500)=n(6500)
Expanding this gives:
7500n+3750=6500n
Step 6: Solve for n
Rearranging the equation:
7500n−6500n=−3750
1000n=−3750
n=37501000=3.75
Step 7: Use n to Find Thickness t
Now we can use either equation to find t. Let’s use the minima equation:
2μt=nλmin
Substituting μ and n:
2(53)t=3.75×(6500×10−10)
103t=3.75×6500×10−10
Step 8: Calculate t
Calculating the right side:
t=3.75×6500×10−10×310
Calculating the numerical value:
t=24375×10−10×310=7.3125×10−7m=7.3125×10−7m
Final Answer
The thickness of the film is approximately:
t≈7.31×10−7m
For a thin film, the conditions for maxima and minima are given by:
- For maxima: 2μt=(n+12)λmax
- For minima: 2μt=nλmin
- μ is the refractive index of the film,
- t is the thickness of the film,
- n is an integer (order of interference),
- λmax and λmin are the wavelengths of light corresponding to maxima and minima respectively.
From the problem:
- λmin=6500Å=6500×10−10m
- λmax=7500Å=7500×10−10m
- μ=53
1. 2μt=(n+12)λmax
2. 2μt=nλmin
Since both expressions are equal to 2μt, we can set them equal to each other:
(n+12)λmax=nλmin
Substituting the values of λmax and λmin:
(n+12)(7500×10−10)=n(6500×10−10)
Cancelling 10−10 from both sides:
(n+12)(7500)=n(6500)
Expanding this gives:
7500n+3750=6500n
Rearranging the equation:
7500n−6500n=−3750
1000n=−3750
n=37501000=3.75
Now we can use either equation to find t. Let’s use the minima equation:
2μt=nλmin
Substituting μ and n:
2(53)t=3.75×(6500×10−10)
103t=3.75×6500×10−10
Calculating the right side:
t=3.75×6500×10−10×310
Calculating the numerical value:
t=24375×10−10×310=7.3125×10−7m=7.3125×10−7m
The thickness of the film is approximately:
t≈7.31×10−7m
Similar Questions
White light reflected from a soap film (Refractive index =1.5 ) has a maxima at 600 nm and a minima at 450 nm at with no minimum in between. Then, the thickness of the film is
View SolutionA plane wave of monochromatic light falls normally on a uniform thin or oil which covers a glass plate. The wavelength of source can be varied continuously. Complete destructive is observed for λ=5000Å and λ=1000Å and for no other wavelength in between. If μ of oil is 1.3 and that of glass is 1.5, the thickness of the film will be
View Solution
Knowledge Check
The colours seen in the reflected white light from a thin oil film are due to
ADiffractionBInterferenceCPolarisationDDispersion
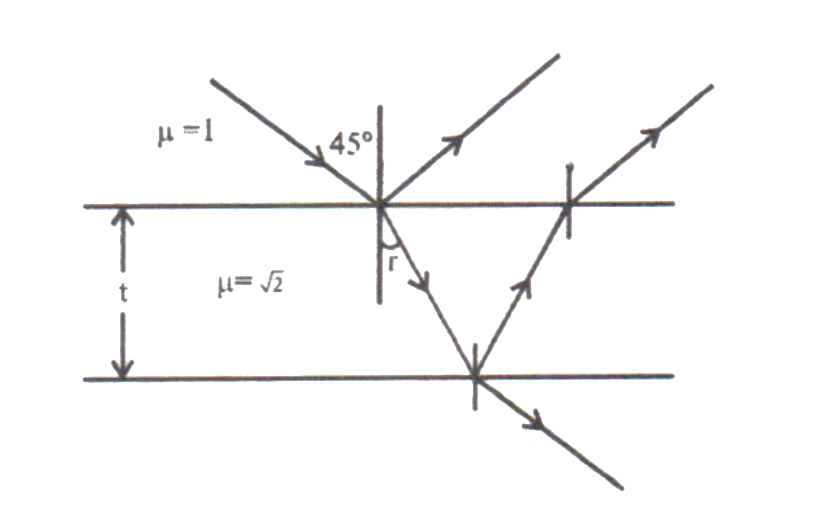
A ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
View SolutionAn oil film (n=1.45) floating on water is illuminated by white light at normal incidence. The film is 280 nm thick. Find (a) the color or the light in the visible specturm most strongly reflected and (b) the color of the light in the specturm most strongly transmitted. Explain your reasoning.
View SolutionBlue light of wavelength 480 nm is most strongly reflected off a thin film of oil on a glass slab when viewed near normal incidence. Assuming that the index of refraction of the oil is 1.2 and that of the glass is 1.6, what is the minimum thickness of the oil film (other then zero)?
View SolutionYDSE is carried out in a liquid of refractive index μ=1.3 and a thin film of air is formed in front of the lower slit as shown in the figure. If a maxima of third order is formed at the origin O, find the thickness of the air film. Find the positions of the fourth maxima. The wavelength of light is air is λ0=0.78μm and D/d=1000.
View SolutionA soap film of thickness t is surrounded by air and is illuminated at near normal incidence by monochromatic light wavelength λ in the film. With respect to the wavelength of the monochromatic light in the film, what film thickness will produce maximum constructive interference
View SolutionA 600 nm light is perpendicularly incident on a soap film suspended air. The film is 1.00μm thick with n=1.35. Which statement most accurately describes the interference of light reflected by the two surfaces of the film?
View SolutionA prism (μP=√3) has an angle of prism A=30∘.A thin film (μf=2.2) is coated on face AC as shown in the figure.Light of wavelength 550nm is incident on the face ABat60∘angle of incidence,find
(I)the angle of its emergence from the faceACand

(ii)the minimum thickness (in mn) of the film for which the emerging light is of maximum possible intensity.
View Solution
