The mass of a pendulum bob is m = 2kg and the length of the string is l. It is displaced through 90∘ from the vertical and released. What minimum tension (in N) should the string should be able to withstand so that it doesn't break during motion?
The correct Answer is:60
To solve the problem of determining the minimum tension that the string of a pendulum should withstand when the bob is displaced through 90∘ from the vertical and released, we can follow these steps:
Step 1: Understand the Initial Conditions
The pendulum bob has a mass m=2kg and is displaced to an angle of 90∘ from the vertical. At this position, the bob is at its maximum height.
Step 2: Calculate the Height
When the pendulum is at 90∘, the height h above the lowest point can be calculated using the length of the string l:
h=l
Step 3: Use Conservation of Energy
At the highest point, all the energy is potential energy (PE), which can be expressed as:
PE=mgh=mg⋅l
When the pendulum bob swings down to the lowest point, this potential energy converts into kinetic energy (KE):
KE=12mv2
By conservation of energy:
mgl=12mv2
Cancelling m from both sides (since m≠0):
gl=12v2
Step 4: Solve for Velocity
Rearranging the equation gives:
v2=2gl
Step 5: Analyze Forces at the Lowest Point
At the lowest point of the swing, the forces acting on the bob are:
1. The tension T in the string acting upwards.
2. The weight mg acting downwards.
Using Newton's second law, the net force acting on the bob at the lowest point is:
T−mg=mv2l
Substituting v2 from the previous step:
T−mg=m(2gl)l
This simplifies to:
T−mg=2mg
Step 6: Solve for Tension
Rearranging gives:
T=2mg+mg=3mg
Substituting m=2kg and g=10m/s2:
T=3⋅2⋅10=60N
Conclusion
The minimum tension that the string should be able to withstand is:
60N
The pendulum bob has a mass m=2kg and is displaced to an angle of 90∘ from the vertical. At this position, the bob is at its maximum height.
When the pendulum is at 90∘, the height h above the lowest point can be calculated using the length of the string l:
h=l
At the highest point, all the energy is potential energy (PE), which can be expressed as:
PE=mgh=mg⋅l
When the pendulum bob swings down to the lowest point, this potential energy converts into kinetic energy (KE):
KE=12mv2
By conservation of energy:
mgl=12mv2
Cancelling m from both sides (since m≠0):
gl=12v2
Rearranging the equation gives:
v2=2gl
At the lowest point of the swing, the forces acting on the bob are:
1. The tension T in the string acting upwards.
2. The weight mg acting downwards.
T−mg=mv2l
Substituting v2 from the previous step:
T−mg=m(2gl)l
This simplifies to:
T−mg=2mg
Rearranging gives:
T=2mg+mg=3mg
Substituting m=2kg and g=10m/s2:
T=3⋅2⋅10=60N
The minimum tension that the string should be able to withstand is:
60N
Similar Questions
The string of pendulum of length l is displaced through 90∘ from the vertical and released. Then the minimum strength of the string in order to withstand the tension, as the pendulum passes through the mean position is
View SolutionA pendulum bob on a 2 m string is displaced 60∘ from the vertical and then released. What is the speed of the bob as it passes through the lowest point in its path
View SolutionA pendulum consists of a small mass m at the end of a string of length L. The pendulum is pulled aside making an angle θ with the vertical and released. Taking the suspension point as the axis, at the instant of release
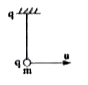
View SolutionA point mass m connected to one end of inextensible string of length l and other end of string is fixed at peg. String is free to rotate in vertical plane. Find the minimum velocity given to the mass in horizontal direction so that it hits the peg in its subsequent motion.
View SolutionA 2 kg stone tied at the end of a string of l m len"gt"h, is whirled along a vertical circle at a constant speed of 4ms−1. The tension in the string has a value of 52 N when the stone is
View SolutionA bob hangs from a rigid support by an inextensible string of length l. If it is displaced through a distance l (from the lowest position) keeping the string straight and then released. The speed of the bob at the lowest position is

View SolutionThe both of a pendulum has mass m = 1 kg and charge q=40μC. Length of pendulum is = 0.9 m. The point of suspensison also has the same charge 40μC. What is the minimum speed u (in m/s) should be imparted to the bob so that it can complete vertical circle ?
View SolutionA stone of mass 2.0 kg is tied to the end of a string of 2m length. It is whirled in a horizontal circle. If the breaking tension of the string is 400 N, calculate the maximum velocity of the stone.
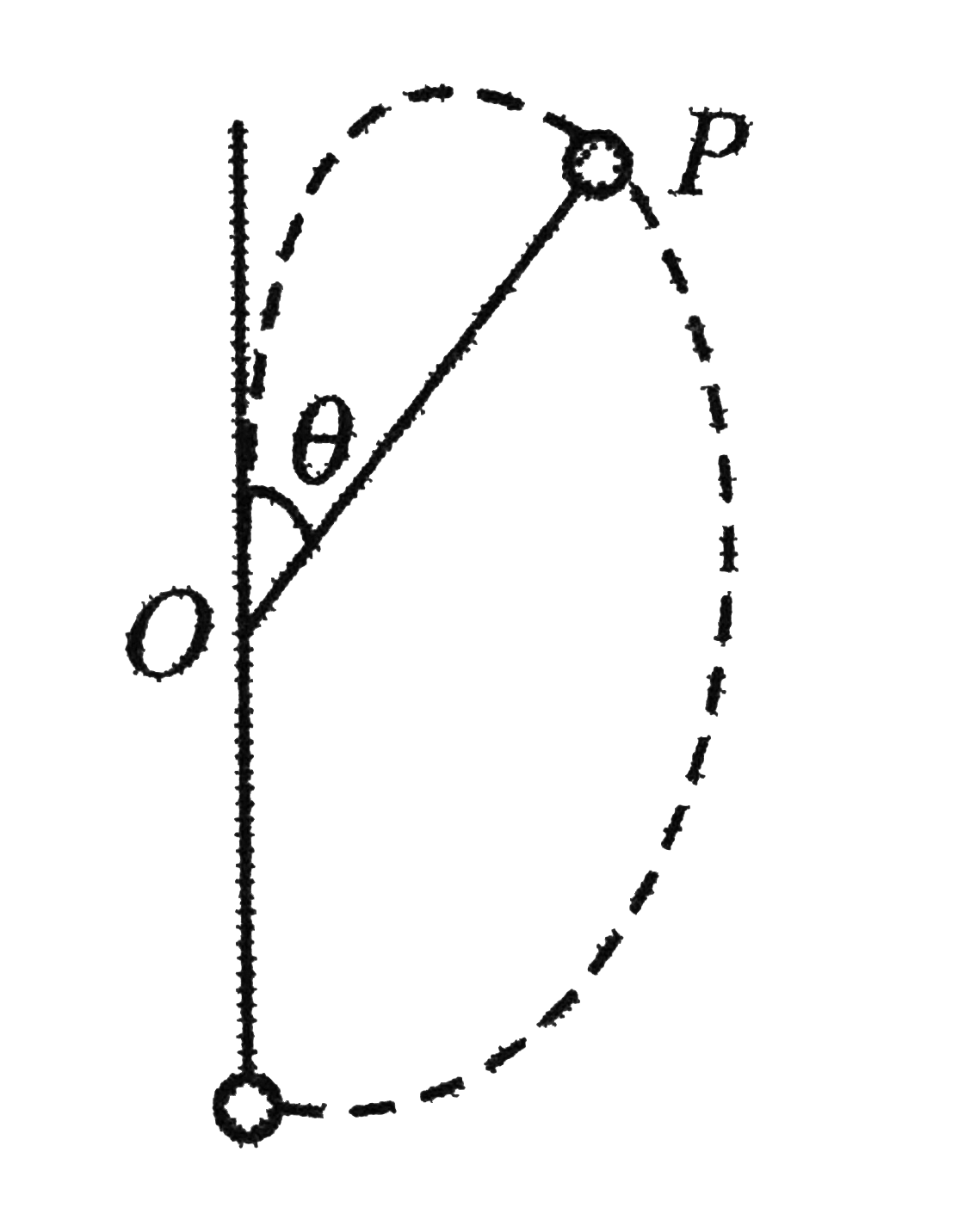
View SolutionA simple pendulum of bob of mass m and length L has one of its ends fixed at the centre O of a vertical circle, as shown in the figure. If 0=60∘ at the point P, the minimum speed u that should be given to the bob so that it completes vetical circle is
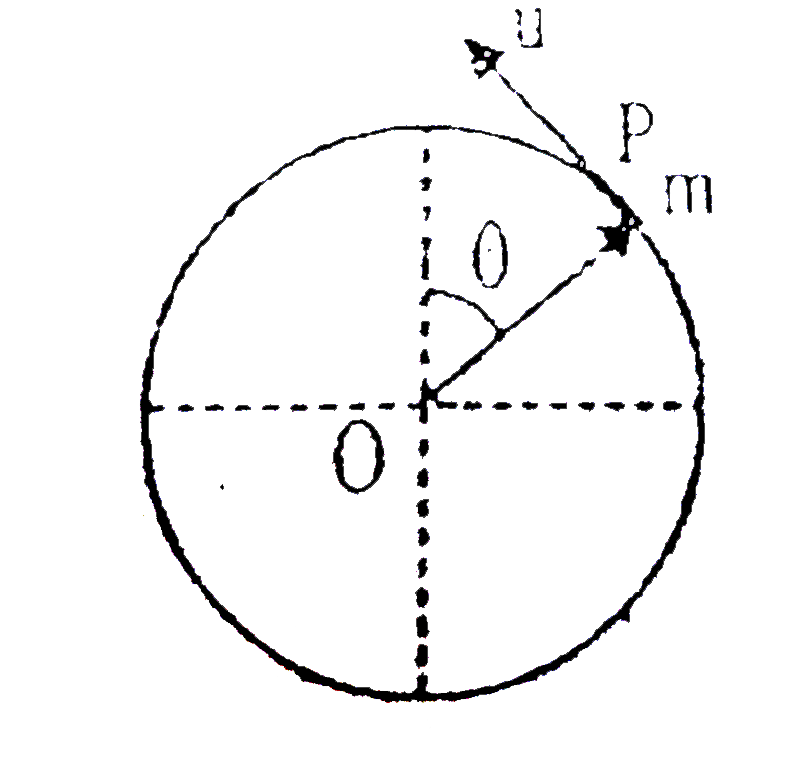
View SolutionOne end of string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lowermost.point so that the string does not slack at any point in its motion along the vertical circle ?
View Solution
