A constant power is suppied to a rotating disc. The relationship between the angular velocity (ω) of the disc and number of rotations (n) made by the disc is governed by
13
32
23
2
The correct Answer is:A
To solve the problem of finding the relationship between the angular velocity (ω) of a rotating disc and the number of rotations (n) made by the disc when a constant power is supplied, we can follow these steps:
1. Define the Power and Energy Relationship:
- Given that a constant power P is supplied to the rotating disc, the energy E acquired by the disc over time t can be expressed as:
E=P⋅t(Equation 1)
2. Express the Rotational Energy:
- The energy of rotation for a disc with moment of inertia I and angular velocity ω is given by:
E=12Iω2(Equation 2)
3. Equate the Two Energy Expressions:
- Setting the two expressions for energy equal to each other gives:
P⋅t=12Iω2
4. Differentiate with Respect to Time:
- Differentiate both sides with respect to time t:
ddt(P⋅t)=ddt(12Iω2)
- This results in:
P=12I⋅2ωdωdt⟹P=Iωdωdt
5. Rearranging the Equation:
- Rearranging gives:
dωdt=PIω
6. Express in Terms of Angular Position:
- Multiply and divide by dθ (the change in angular position):
dωdθ⋅dθdt=PIω
- Since dθdt=ω, we have:
ωdωdθ=PI
7. Separate Variables:
- Rearranging gives:
ω2dω=PIdθ
8. Integrate Both Sides:
- Integrate from 0 to ω on the left and from 0 to 2nπ on the right:
∫ω0ω2dω=PI∫2nπ0dθ
- This results in:
ω33=PI(2nπ)
9. Solve for ω:
- Rearranging gives:
ω3=6nπPI
- Taking the cube root:
ω=(6nπPI)1/3
10. Establish the Relationship:
- From the above expression, we can see that ω is proportional to n1/3:
ω∝n1/3
Conclusion:
The relationship between the angular velocity ω of the disc and the number of rotations n made by the disc is given by:
ω∝n1/3
- Given that a constant power P is supplied to the rotating disc, the energy E acquired by the disc over time t can be expressed as:
E=P⋅t(Equation 1)
- The energy of rotation for a disc with moment of inertia I and angular velocity ω is given by:
E=12Iω2(Equation 2)
- Setting the two expressions for energy equal to each other gives:
P⋅t=12Iω2
- Differentiate both sides with respect to time t:
ddt(P⋅t)=ddt(12Iω2)
- This results in:
P=12I⋅2ωdωdt⟹P=Iωdωdt
- Rearranging gives:
dωdt=PIω
- Multiply and divide by dθ (the change in angular position):
dωdθ⋅dθdt=PIω
- Since dθdt=ω, we have:
ωdωdθ=PI
- Rearranging gives:
ω2dω=PIdθ
- Integrate from 0 to ω on the left and from 0 to 2nπ on the right:
∫ω0ω2dω=PI∫2nπ0dθ
- This results in:
ω33=PI(2nπ)
- Rearranging gives:
ω3=6nπPI
- Taking the cube root:
ω=(6nπPI)1/3
- From the above expression, we can see that ω is proportional to n1/3:
ω∝n1/3
The relationship between the angular velocity ω of the disc and the number of rotations n made by the disc is given by:
ω∝n1/3
Similar Questions
Knowledge Check
When a disc rotates with uniform angular velocity, which of the following is not true ?
Aa. The sense of rotation remains same.Bb. The orientation of the axis of rotation remains same.Cc. The speed of rotation is non-zero and remains same.Dd. The angular acceleration is non-zero and remains same.
A disc is rotaing with an angular velocity ω0. A constant retarding torque is applied on it to stop the disc. The angular velocity becomes ω02 after n rotations. How many more rotations will it make before coming to rest ?
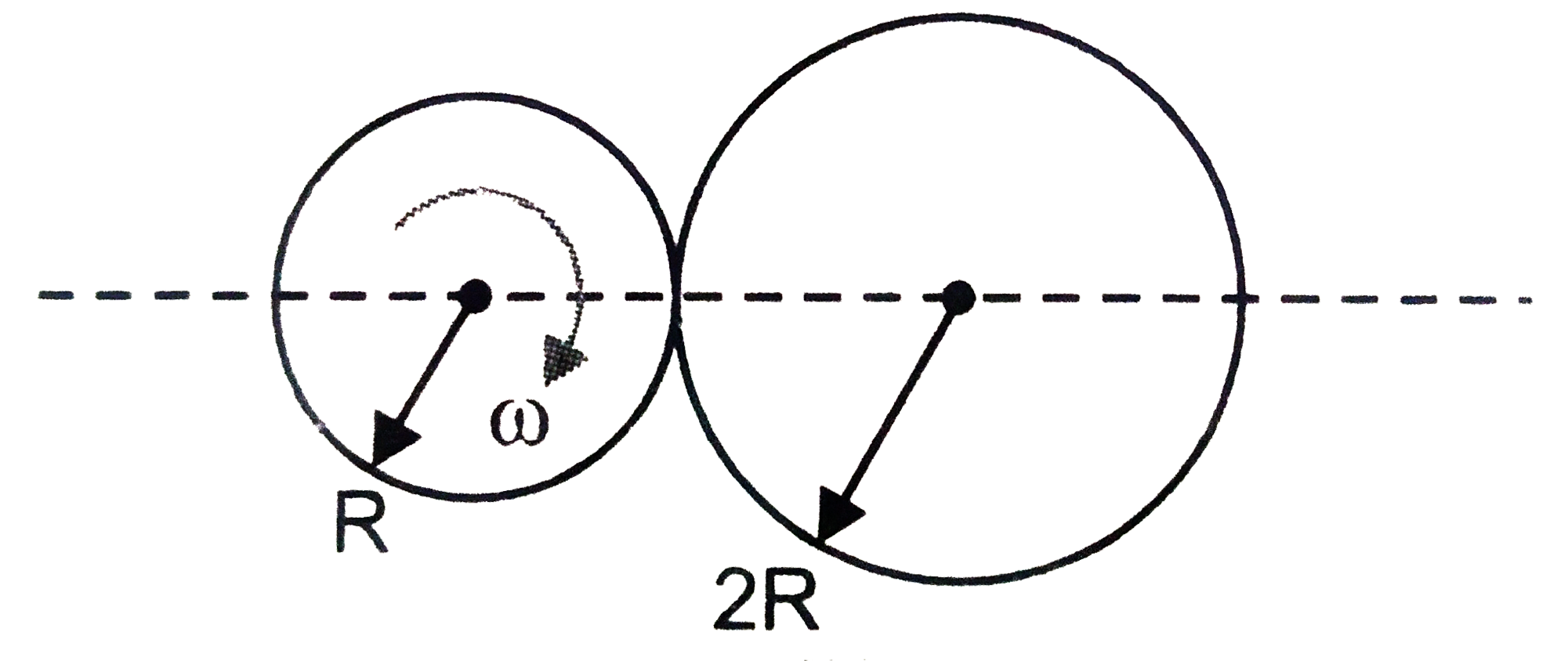
View SolutionTwo discs of radii Rand2R are pressed against each other. Initially, disc with radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertia of smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
View SolutionA cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
View SolutionA circular disc is rotating about its own axis at uniform angular velocity ω. The disc is subjected to uniform angular retardation by which its angular velocity is decreased to ω/2 during 120 rotations., The number of rotations further made by it before coming to rest is
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is

View SolutionWhen a disc rotates with uniform angular velocity, which of the following is not true ?
View SolutionTwo discs are mounted on frictionless bearings on a common shaft. The first disc has rotational inertia / and is spinning with angular velocity ω. The second disc has rotational inertia 2/ and is spinning in opposite direction with angular velocity 3ω, as shown in figure. The two discs are slowly forced towards each other along the shaft until they couple and have a final common angular velocity of

View Solution
