In a meter-bridge experiment with a resistance R1 in left gap and a resistance X in a right gap. null point is obtained at 40cm from the left emf. With a resistance R2 in the left gap, the null point is obtainned at 50cm from left hand. Find the position of the left gap is containing R1 and R2 (i) in series and (ii) in parallel.
The correct Answer is:62.5
To solve the problem step by step, we will analyze the two cases: when the resistances R1 and R2 are in series and when they are in parallel.
Given:
1. Null point with R1 in left gap and X in right gap is at 40cm.
2. Null point with R2 in left gap and X in right gap is at 50cm.
Step 1: Finding the relationship between R1 and X
Using the principle of the meter bridge, we have:
R1X=4060
This simplifies to:
R1=23X(Equation 1)
Step 2: Finding the relationship between R2 and X
Similarly, for the second case:
R2X=5050
This simplifies to:
R2=X(Equation 2)
Step 3: Case (i) - R1 and R2 in series
When R1 and R2 are in series, the equivalent resistance Req is:
Req=R1+R2=23X+X=53X
Using the balance condition again:
ReqX=L1100−L1
Substituting Req:
53XX=L1100−L1
This simplifies to:
53=L1100−L1
Step 4: Cross-multiplying to solve for L1
Cross-multiplying gives:
5(100−L1)=3L1
Expanding and rearranging:
500−5L1=3L1⟹500=8L1⟹L1=5008=62.5cm
Step 5: Case (ii) - R1 and R2 in parallel
For resistances in parallel, the equivalent resistance Req is given by:
1Req=1R1+1R2
Substituting R1 and R2:
1Req=32X+1X=3+22X=52X
Thus,
Req=2X5
Using the balance condition:
ReqX=L2100−L2
Substituting Req:
2X5X=L2100−L2
This simplifies to:
25=L2100−L2
Step 6: Cross-multiplying to solve for L2
Cross-multiplying gives:
2(100−L2)=5L2
Expanding and rearranging:
200−2L2=5L2⟹200=7L2⟹L2=2007≈28.57cm
Final Answers:
1. When R1 and R2 are in series, the null point is at L1=62.5cm.
2. When R1 and R2 are in parallel, the null point is at L2≈28.57cm.
1. Null point with R1 in left gap and X in right gap is at 40cm.
2. Null point with R2 in left gap and X in right gap is at 50cm.
R1X=4060
This simplifies to:
R1=23X(Equation 1)
R2X=5050
This simplifies to:
R2=X(Equation 2)
Req=R1+R2=23X+X=53X
ReqX=L1100−L1
Substituting Req:
53XX=L1100−L1
This simplifies to:
53=L1100−L1
5(100−L1)=3L1
Expanding and rearranging:
500−5L1=3L1⟹500=8L1⟹L1=5008=62.5cm
1Req=1R1+1R2
Substituting R1 and R2:
1Req=32X+1X=3+22X=52X
Thus,
Req=2X5
ReqX=L2100−L2
Substituting Req:
2X5X=L2100−L2
This simplifies to:
25=L2100−L2
2(100−L2)=5L2
Expanding and rearranging:
200−2L2=5L2⟹200=7L2⟹L2=2007≈28.57cm
1. When R1 and R2 are in series, the null point is at L1=62.5cm.
2. When R1 and R2 are in parallel, the null point is at L2≈28.57cm.
Similar Questions
In a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
View SolutionIn a meter bridge circuit, resistance, in the left hand gap is 2Ω and an unknown resistance X is in the right hand gap as shown in figure below. The null point is found to be 40 cm from the left end of the wire. What resistance should be connected to X so that the new null point is 50 cm from the left end of the wire ?
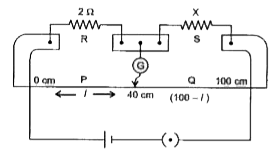
View Solution
Knowledge Check
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
In the metrebridge experiment , the null point is obtained at N. The value of unkonw resistance X will be .
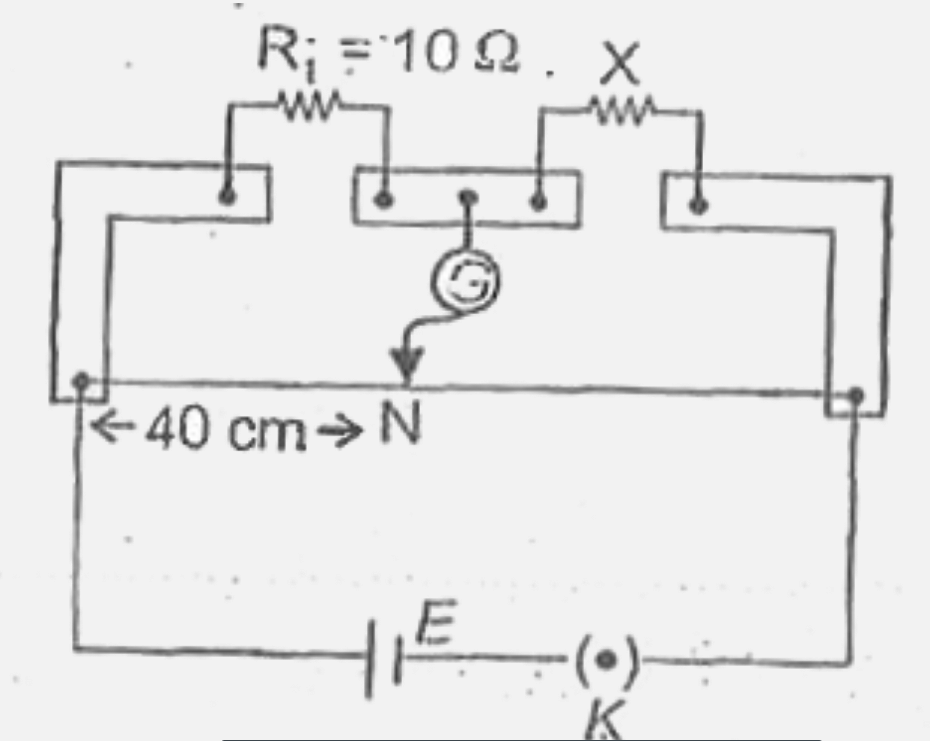
View SolutionIn a meter bridge, the null point is found at a distance of 40cm from A. If a resistance of 12Ω in connected in parallel with S the null point occurs at 50.0cm from A Determine the value of R and S

View SolutionIn a meter bridge, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10 cm. Find the unknown resistance X.
View SolutionIn a meter bridge, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10 cm. Find the unknown resistance X.
View SolutionIn a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.

View SolutionIn a meter bride, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10cm . Find the unknown resistance X.
View SolutionIn a metre bridge, the gaps are closed by two resistance P and Q and the balance point is obtained at 40cm. When Q is shunted by a resistance of 10Ω, the balance point shifts to 50cm. The values of P and Q are.
 .
.
View Solution
