In a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
The correct Answer is:22.5cm
To solve the problem step by step, we will follow the principles of the meter bridge and the concept of parallel resistances.
Step 1: Understand the initial setup
In the meter bridge, we have:
- Resistance R1=2Ω (left gap)
- Unknown resistance R0 (right gap)
- Balance point at x=40cm
Step 2: Use the balance condition
According to the principle of the meter bridge, the balance point is given by the relation:
R1R0=x100−x
Substituting the known values:
2R0=40100−40
This simplifies to:
2R0=4060=23
Step 3: Solve for the unknown resistance R0
Cross-multiplying gives:
2⋅3=2⋅R0
R0=3Ω
Step 4: Introduce the shunt resistance
Now, we shunt the unknown resistance R0 with 2Ω. The equivalent resistance R′0 can be calculated using the formula for resistances in parallel:
R′0=R0⋅2R0+2
Substituting R0=3Ω:
R′0=3⋅23+2=65Ω
Step 5: Find the new balance point
Now, we need to find the new balance point x′ using the new resistance R′0:
R1R′0=x′100−x′
Substituting the values:
265=x′100−x′
This simplifies to:
2⋅56=x′100−x′
53=x′100−x′
Step 6: Cross-multiply to find x′
Cross-multiplying gives:
5(100−x′)=3x′
Expanding this:
500−5x′=3x′
Combining like terms:
500=8x′
Thus, we find:
x′=5008=62.5cm
Step 7: Calculate the shift in the balance point
The shift in the balance point is given by:
Shift=x′−x=62.5cm−40cm=22.5cm
Final Answer
The shift of the balance point on the bridge wire is 22.5cm.
---
In the meter bridge, we have:
- Resistance R1=2Ω (left gap)
- Unknown resistance R0 (right gap)
- Balance point at x=40cm
According to the principle of the meter bridge, the balance point is given by the relation:
R1R0=x100−x
Substituting the known values:
2R0=40100−40
This simplifies to:
2R0=4060=23
Cross-multiplying gives:
2⋅3=2⋅R0
R0=3Ω
Now, we shunt the unknown resistance R0 with 2Ω. The equivalent resistance R′0 can be calculated using the formula for resistances in parallel:
R′0=R0⋅2R0+2
Substituting R0=3Ω:
R′0=3⋅23+2=65Ω
Now, we need to find the new balance point x′ using the new resistance R′0:
R1R′0=x′100−x′
Substituting the values:
265=x′100−x′
This simplifies to:
2⋅56=x′100−x′
53=x′100−x′
Cross-multiplying gives:
5(100−x′)=3x′
Expanding this:
500−5x′=3x′
Combining like terms:
500=8x′
Thus, we find:
x′=5008=62.5cm
The shift in the balance point is given by:
Shift=x′−x=62.5cm−40cm=22.5cm
The shift of the balance point on the bridge wire is 22.5cm.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-6
5 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-A
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-3
4 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
Similar Questions
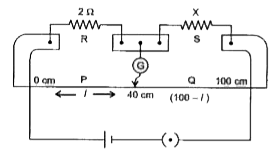
In a meter bridge circuit, resistance, in the left hand gap is 2Ω and an unknown resistance X is in the right hand gap as shown in figure below. The null point is found to be 40 cm from the left end of the wire. What resistance should be connected to X so that the new null point is 50 cm from the left end of the wire ?
View SolutionIn a meter-bridge experiment with a resistance R1 in left gap and a resistance X in a right gap. null point is obtained at 40cm from the left emf. With a resistance R2 in the left gap, the null point is obtainned at 50cm from left hand. Find the position of the left gap is containing R1 and R2 (i) in series and (ii) in parallel.
View Solution
Knowledge Check
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
When a conducting wire is connected in the left gap and known resistance in the right gap, the balance length is 75cm. If the wire is cut into 3 equal parts and one part isconnected in the left gap, the balance length
View SolutionA student performs meter bridge experiment to determine specific resistance of a conducting wire of length 10cm and diameter 1mm. When a standard 6Ω resistance is connected on left gap and the given conducting wire is connected on the right gap, the balance points obtained for 60cm length of the meter bridge wire. The specific resistance in Ω−m for material of the given wire is:
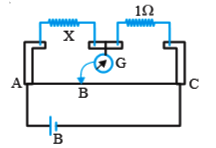
View SolutionIn the metre bridge, the balancing length AB = 20 cm. The unknown resistance X is equal to
View SolutionIn a metre bridge, the gaps are closed by two resistance P and Q and the balance point is obtained at 40cm. When Q is shunted by a resistance of 10Ω, the balance point shifts to 50cm. The values of P and Q are.
 .
.
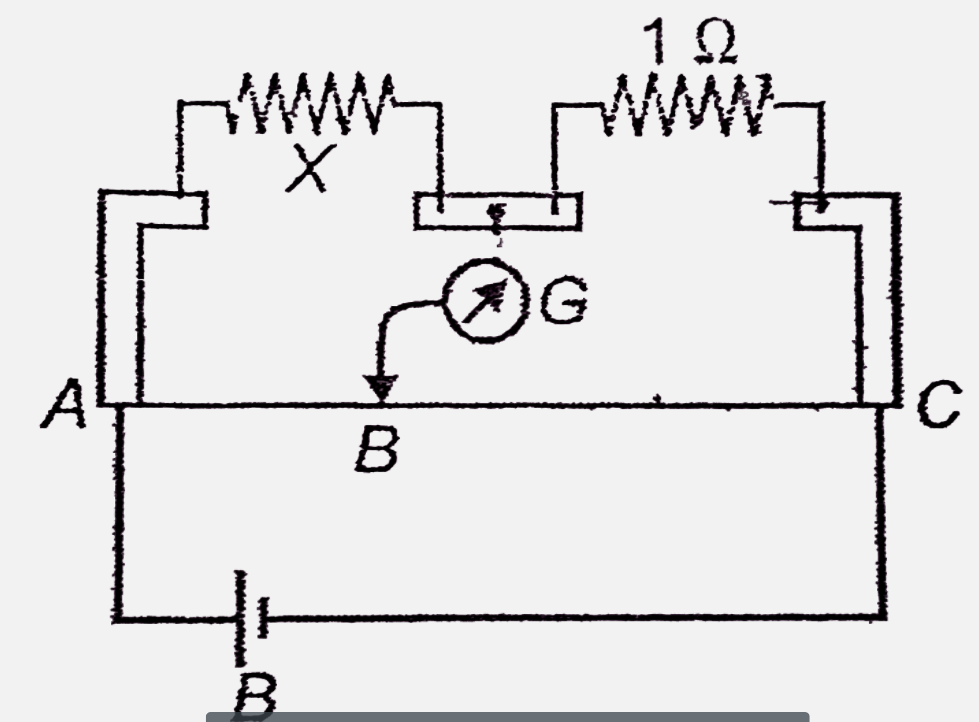
View SolutionIn the metre bridge, the balancing length AB =l=20 cm. The unknown resistance X is equal to
View SolutionIn an experiment to determine an unknown resistance, a 100 cm long resistance wire is used. The unknown resistance is kept in the left gap and a known resistance is put into the right gap. The scale to measure length has a least count 1 mm. The null point B is obtained at 40.0 cm from the left gap. We shell determine the percentage error in the computation of unknown resistance.
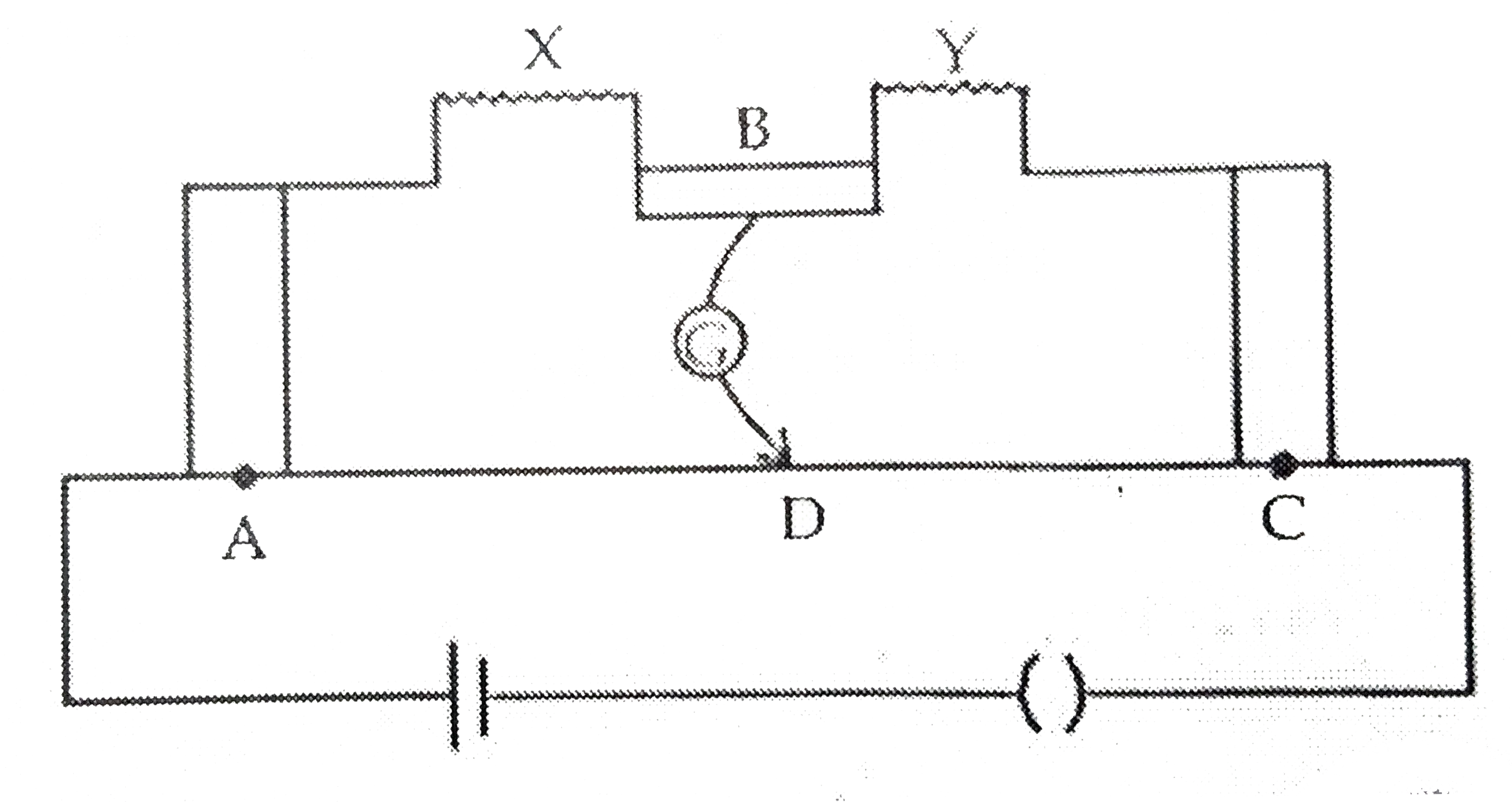
View SolutionThe figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead connected in series with resistance 'Y'. Determine the value of the resistance X and Y
View Solution
