Question

Which of the following is correct representation of the variation of half - life with initial concentration of a zero order reaction ?

Options

A.
B.
C.
D.

Answer

A

Explanation

To solve the problem regarding the variation of half-life with initial concentration in a zero-order reaction, we can follow these steps:

1. Understand the Zero-Order Reaction Equation:
The rate law for a zero-order reaction can be expressed as:
\( (A)_t = (A)_0 - kt \)
where:
- \((A)_t\) is the concentration at time \(t\),
- \((A)_0\) is the initial concentration,
- \(k\) is the rate constant,
- \(t\) is time.

2. Determine the Half-Life Expression:
The half-life (\(t_{1/2}\)) for a zero-order reaction is the time required for the concentration of the reactant to decrease to half of its initial concentration. At half-life:
\( (A)_{t_{1/2}} = \frac{(A)_0}{2} \)

3. Set Up the Equation for Half-Life:
Substitute \((A)_{t_{1/2}}\) into the zero-order reaction equation:
\( \frac{(A)_0}{2} = (A)_0 - kt_{1/2} \)

4. Rearrange the Equation:
Rearranging gives:
\( kt_{1/2} = (A)_0 - \frac{(A)_0}{2} \)
Simplifying this, we find:
\( kt_{1/2} = \frac{(A)_0}{2} \)

5. Solve for Half-Life:
Now, we can express the half-life in terms of the initial concentration:
\( t_{1/2} = \frac{(A)_0}{2k} \)

6. Analyze the Relationship:
From the equation \(t_{1/2} = \frac{(A)_0}{2k}\), we can see that:
- \(t_{1/2}\) is directly proportional to the initial concentration \((A)_0\) since \(2k\) is a constant.

7. Graphical Representation:
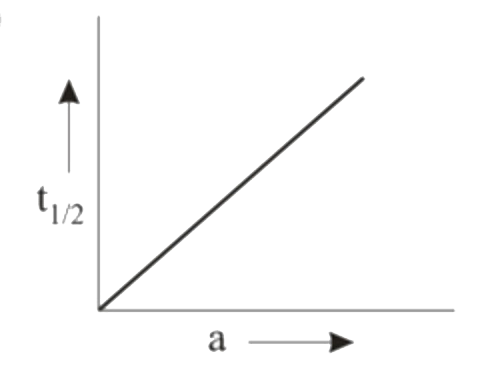
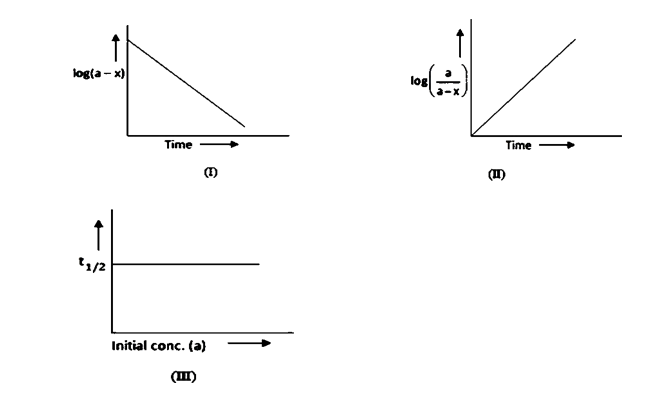
Since \(t_{1/2}\) increases linearly with \((A)_0\), the graph of half-life (\(t_{1/2}\)) versus initial concentration (\((A)_0\)) will be a straight line.

Conclusion:
The correct representation of the variation of half-life with initial concentration of a zero-order reaction is a straight line graph, indicating that half-life is directly proportional to the initial concentration.