Mg(s)∣∣Mg2+(aq)∣∣∣∣Zn2+(aq)∣∣Zn(s),E∘=+3.13V
The correct plot of Ecell versus log.[Mg2+][Zn2+] will be represented as
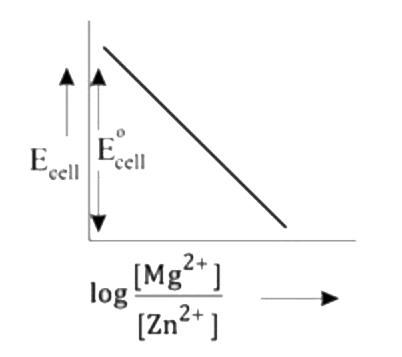
The correct Answer is:B
To solve the problem, we need to analyze the given electrochemical cell and apply the Nernst equation to determine how the cell potential (E_cell) varies with the logarithm of the concentration ratio of magnesium ions to zinc ions.
1. Identify the Cell Reaction:
The cell is represented as:
Mg(s)|Mg2+(aq)||Zn2+(aq)|Zn(s)
The half-reactions are:
- Oxidation: Mg→Mg2++2e−
- Reduction: Zn2++2e−→Zn
2. Write the Overall Cell Reaction:
The overall cell reaction can be written as:
Mg+Zn2+→Mg2++Zn
3. Apply the Nernst Equation:
The Nernst equation for the cell potential is given by:
Ecell=E∘cell−0.0591nlog((Mg2+)(Zn2+))
Where:
- E∘cell=+3.13V (given)
- n=2 (number of electrons transferred)
4. Substitute Values into the Nernst Equation:
Substituting the values into the Nernst equation:
Ecell=3.13−0.05912log((Mg2+)(Zn2+))
Simplifying gives:
Ecell=3.13−0.02955log((Mg2+)(Zn2+))
5. Identify the Plot Characteristics:
- On the y-axis, we have Ecell.
- On the x-axis, we have log((Mg2+)(Zn2+)).
- The slope of the line is negative (−0.02955), indicating that as the log ratio increases, the cell potential decreases.
6. Determine the Correct Plot:
Since the slope is negative, the correct plot of Ecell versus log((Mg2+)(Zn2+)) will be a straight line with a negative slope.
Conclusion:
The correct option for the plot of Ecell versus log((Mg2+)(Zn2+)) is the one that shows a negative slope, which corresponds to option 2.
The cell is represented as:
Mg(s)|Mg2+(aq)||Zn2+(aq)|Zn(s)
The half-reactions are:
- Oxidation: Mg→Mg2++2e−
- Reduction: Zn2++2e−→Zn
The overall cell reaction can be written as:
Mg+Zn2+→Mg2++Zn
The Nernst equation for the cell potential is given by:
Ecell=E∘cell−0.0591nlog((Mg2+)(Zn2+))
Where:
- E∘cell=+3.13V (given)
- n=2 (number of electrons transferred)
Substituting the values into the Nernst equation:
Ecell=3.13−0.05912log((Mg2+)(Zn2+))
Simplifying gives:
Ecell=3.13−0.02955log((Mg2+)(Zn2+))
- On the y-axis, we have Ecell.
- On the x-axis, we have log((Mg2+)(Zn2+)).
- The slope of the line is negative (−0.02955), indicating that as the log ratio increases, the cell potential decreases.
Since the slope is negative, the correct plot of Ecell versus log((Mg2+)(Zn2+)) will be a straight line with a negative slope.
The correct option for the plot of Ecell versus log((Mg2+)(Zn2+)) is the one that shows a negative slope, which corresponds to option 2.
Similar Questions
The cell reaction Zn(s)+Cu+2→Zn+2+Cu(s) is best represented as :
View SolutionFor the galvanic cell Mg(s)∣∣Mg2+(aq)∣∣∣∣Zn2+(aq)∣∣Zn(s),the standard free energy change is (Given:E∘mg2+mg=-2.36V,E∘Zn2+Zn=-0.76V)
View SolutionFor the galvanic cell Zn(s)∣∣Zn2+∣∣∣∣Cd2+∣∣Cd(s),Ecell=0.30VandEocell=0.36V, then value of [Cd2+]/[Zn2+] will be:
View SolutionZn(s)+Cu2+(aq)→Zn2+(aq)+Cu(s) The cell representation for the above redox reaction is
View SolutionCalculate the emf of the cell.
Mg(s)∣∣Mg2+(0.2M)∣∣∣∣Ag+(1×10−3)∣∣Ag
E∘Ag+/Ag=+0.8 volt, E∘Mg2+/Mg=−2.37 volt
What will be the effect on emf If concentration of Mg2+ ion is decreased to 0.1M ?
View SolutionThe standard electrode potential of the half cells are given below :
Zn2++2e−→Zn(s),Eo=−7.62V
Fe2++2e−→Fe(s),Eo=−7.81V
The emf of the cell Fe2++Zn→Zn2++Fe will be :
View SolutionIf E0MgMg2+=+2.37 and E0CuCu2+=−0.34V then standard EMF of the cell, MgMg2+/Cu2+Cu is
View SolutionZn+Cu2+(aq)→Cu+Zn2+(aq).
Reaction quotient is Q=[Zn2+][Cu2+]⋅E∘cell=1.10V ltb rgt Ecell will be 1.1591 V when :

View SolutionThe equilibrium constant for the reaction Sr(s)+Mg+2(aq)→Sr+2(aq)+Mg(s)is2.69×1012at25∘CTheE∘ for a cel made up of Sr/Sr+2 and Mg+2/Mg half cells is
View SolutionFor the electrochemical cell,
Mg(s)∣∣Mg2+(aq.1M)∣∣∣∣Cu2+(aq.1M)∣∣Cu(s)
the standard emf of the cell is 2.70 V at 300 K. When the concentration of Mg2+ is chaged to x M, the cell potential changes to 2.67 V at 300 K. The value of x is ________ .
(Given FR=11500kV−1. where F is the Faraday constant and R is the gas constant, ln (10) = 2.30)
View Solution