Let there are 4 sections of 25 students each in a coaching class. Now, out of 150 students 100 are to be selected randomly and enrolled in these sections. Then, the probability that the students A and B (both present in 150 students) are selected and placed in the same section, is
1013
16149
233
5149
The correct Answer is:B
To solve the problem, we need to find the probability that two specific students, A and B, are selected from a total of 150 students and placed in the same section of 25 students out of 4 sections.
1. Total Students and Sections: We have 150 students in total and 4 sections, each containing 25 students.
2. Choosing Students: We need to select 100 students out of the 150. However, since we are specifically interested in A and B being in the same section, we will first consider the scenario where A and B are already selected.
3. Selecting A and B: If A and B are selected, we have already chosen 2 students. Therefore, we need to select 23 more students to fill one section of 25 students.
4. Remaining Students: After selecting A and B, there are 148 students left (150 - 2 = 148).
5. Choosing Remaining Students: The number of ways to choose the remaining 23 students from the 148 students is given by the combination formula:
(14823)
6. Total Ways to Choose 25 Students: The total number of ways to choose any 25 students from the original 150 is:
(15025)
7. Calculating Probability: The probability that A and B are selected and placed in the same section can be expressed as:
P(A and B in same section)=(14823)(15025)
8. Simplifying the Probability:
- We can express the combinations in terms of factorials:
(14823)=148!23!⋅(148−23)!=148!23!⋅125!
(15025)=150!25!⋅(150−25)!=150!25!⋅125!
- Thus, the probability becomes:
P(A and B in same section)=148!23!⋅125!150!25!⋅125!=148!⋅25!150!⋅23!
9. Cancelling Factorials: Simplifying further:
- We can cancel 148! and 125!:
P(A and B in same section)=25!150×149×148!=25×24150×149
10. Calculating Final Probability:
- This simplifies to:
P(A and B in same section)=4149
11. Considering All Sections: Since there are 4 sections, we multiply the probability by 4:
P(A and B in any section)=4×4149=16149
Final Answer:
Thus, the probability that students A and B are selected and placed in the same section is:
16149
(14823)
(15025)
P(A and B in same section)=(14823)(15025)
- We can express the combinations in terms of factorials:
(14823)=148!23!⋅(148−23)!=148!23!⋅125!
(15025)=150!25!⋅(150−25)!=150!25!⋅125!
P(A and B in same section)=148!23!⋅125!150!25!⋅125!=148!⋅25!150!⋅23!
- We can cancel 148! and 125!:
P(A and B in same section)=25!150×149×148!=25×24150×149
- This simplifies to:
P(A and B in same section)=4149
P(A and B in any section)=4×4149=16149
Thus, the probability that students A and B are selected and placed in the same section is:
16149
Similar Questions
Refer to Example 5, Section 14.4, Chapter 14. Find the probability that a student of the class was born in August.
View SolutionIn a medical examination of students of a class, the following blood groups are recorded.
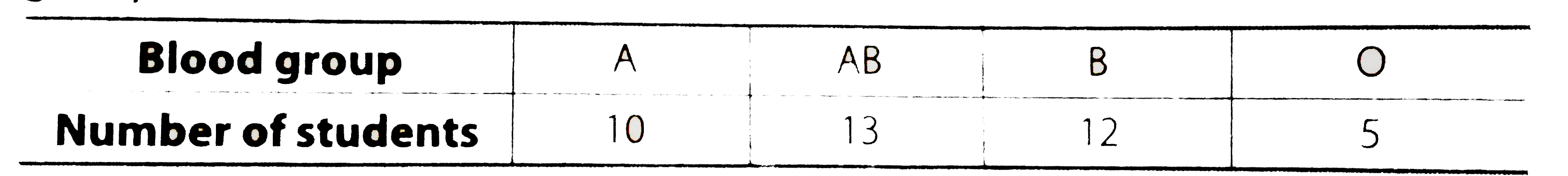
A student is selected at random from the class. The probability that he/she has blood group B, is
View Solution
Knowledge Check
A class has 12 boys and 4 girls. If three students are selected at random from the class,
what is the probability that all will be boys?A155B14C13D1128
A class has 20 girls and 16 boys. One student is selected at random. Find the probability that the student is a girl.
View SolutionIn a class of 50 students, 20 are boys and rest are girls. A student is selected at random. Find the probability of selecting a boy.
View SolutionIn a class of 125 students 70 passed in Mathematics, 55 in statistics, and 30 in both. Then find the probability that a student selected at random from the class has passed in only one subject.
View SolutionIn a class of 125 students 70 passed in Mathematics, 55 in statistics, and 30 in both. Then find the probability that a student selected at random from the class has passes in only one subject.
View SolutionOut of 9 outstanding students in a college, there are 4 boys and 5 girls. A team of four students is to be selected for a quiz programme. Find the probability that two are boys and two are girls.
View SolutionOut of 100 students, two sections of 40 and 60 are formed. If you and your friend are among the 100 students, what is the probability that(a) you both enter the same section?(b) you both enter the different sections?
View Solution100 students appeared for two examinations .60 passed the first , 50 passed the second and 30 passed both . Find the probability that a student selected at random has failed in both examinations .
View Solution
