Two lines $L_{1}$ and $L_{2}$ of slops 1 are tangents to $y^{2} = 4 x$ and $x^{2} + 2 y^{2} = 4$ respectively, such that the distance d units between $L_{1} and L_{2}$ is minimum, then the value of d is equal to

$\sqrt{3} - \frac{1}{\sqrt{2}}$

$\sqrt{3} + \frac{1}{\sqrt{2}}$

$\sqrt{2} - 1$

$\sqrt{3} + \sqrt{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video & image solution for Two lines L_(1) and L_(2) of slops 1 are tangents to y^(2)=4x and x^(2)+2y^(2)=4 respectively, such that the distance d units between L_(1) and L _(2) is minimum, then the value of d is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

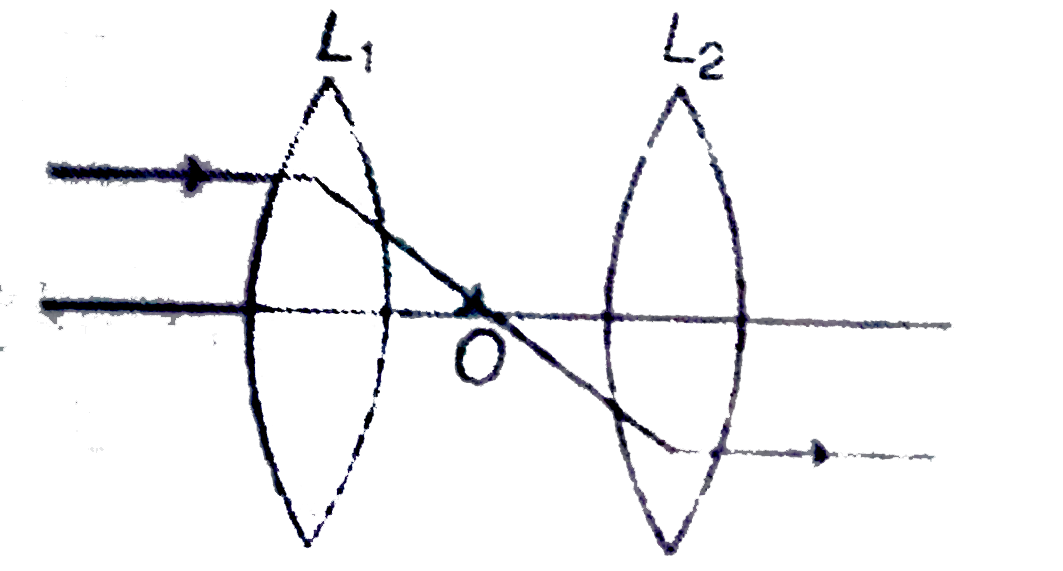
In the figure shown, there are two convex lenses $L_{1}$ and $L_{2}$ having focal. Lengths $f_{1}$ and $f_{2}$ respectively. The distance between $L_{1}$ and $L_{2}$ will be

View Solution
Let $l_{1}$ and $l_{2}$ be the two lines which are normal to $y^{2} = 4 x$ and tangent to $x^{2} = - 12 y$ respectively (where, $l_{1} and l_{2}$ are not the x - axis). Then, the product of the slopes of $l_{1} and l_{2}$ is
View Solution
The combined equation of the lines $L_{1}$ and $L_{2}$ is $2 x^{2} + 6 x y + y^{2} = 0$ and that lines $L_{3}$ and $L_{4}$ is $4 x^{2} + 18 x y + y^{2} = 0$ . If the angle between $L_{1}$ and $L_{4}$ be $α$ , then the angle between $L_{2}$ and $L_{3}$ will be
View Solution
The line $L_{1} \equiv 3 x - 4 y + 1 = 0$ touches the circles $C_{1} and C_{2}$ . Centers of $C_{1}$ and $C_{2}$ are $A_{1} (1, 2)$ and $A_{2} (3, 1)$ respectively Then, the length (in units) of the transverse common tangent of $C_{1} and C_{2}$ is equal to
View Solution
If the lines $L_{1}$ and $L_{2}$ are tangents to $4 x^{2} - 4 x - 24 y + 49 = 0$ and are normals for $x^{2} + y^{2} = 72,$ then find the slopes of $L_{1}$ and $L_{2} .$
View Solution
The lines $L_{1} : y - x = 0$ and $L_{2} : 2 x + y = 0$ intersect the line $L_{3} : y + 2 = 0$ at P and Q respectively . The bisectors of the acute angle between $L_{1}$ and $L_{2}$ intersect $L_{3}$ at R .
Statement 1 : The ratio PR : RQ equals $2 \sqrt{2} : \sqrt{5}$
Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangles .
View Solution
Consider the lines $L_{1} \equiv 3 x - 4 y + 2 = 0 and L_{2} \equiv 3 y - 4 x - 5 = 0 .$ Now, choose the correct statement(s).
(a)The line x+y=0 bisects the acute angle between $L_{1} and L_{2}$ containing the origin.
(b)The line x-y+1=0 bisects the obtuse angle between $L_{1} and L_{2}$ not containing the origin.
(c)The line x+y+3=0 bisects the obtuse angle between $L_{1} and L_{2}$ containing the origin.
(d)The line x-y+1=0 bisects the acute angle between $L_{1} and L_{2}$ not containing the origin.
View Solution
Let the lines $l_{1}$ and $l_{2}$ be normals to $y^{2} = 4 x$ and tangents to $x^{2} = - 12 y$ (where $l_{1} and l_{2}$ are not x - axis). The absolute value of the difference of slopes of $l_{1} and l_{2}$ is
View Solution
The line $L_{1} : \frac{x}{5} + \frac{y}{b} = 1$ passes through the point (13, 32) and is parallel to $L_{2} : \frac{x}{c} + \frac{y}{3} = 1 .$ Then, the distance between $L_{1} and L_{2}$ is
View Solution
The shortest distance between the two lines $L_{1} : x = k_{1}, y = k_{2} and L_{2} : x = k_{3}, y = k_{4}$ is equal to
View Solution

Two lines L1 and L2 of slops 1 are tangents to y2=4x and x2+2y2=4 respectively, such that the distance d units between L1andL2 is minimum, then the value of d is equal to

The correct Answer is:A

Similar Questions

Recommended Questions

Two lines $L_{1}$ and $L_{2}$ of slops 1 are tangents to $y^{2} = 4 x$ and $x^{2} + 2 y^{2} = 4$ respectively, such that the distance d units between $L_{1} and L_{2}$ is minimum, then the value of d is equal to