Consider the lines L1≡3x−4y+2=0 and L2≡3y−4x−5=0. Now, choose the correct statement(s).
(a)The line x+y=0 bisects the acute angle between L1and L2 containing the origin.
(b)The line x-y+1=0 bisects the obtuse angle between L1 and L2 not containing the origin.
(c)The line x+y+3=0 bisects the obtuse angle between L1 and L2 containing the origin.
(d)The line x-y+1=0 bisects the acute angle between L1 and L2 not containing the origin.
The line x+y=0 bisects the acute angle between L1and L2 containing the origin.
The line x-y+1=0 bisects the obtuse angle between L1 and L2 not containing the origin.
The line x+y+3=0 bisects the obtuse angle between L1 and L2 containing the origin.
The line x-y+1=0 bisects the acute angle between L1 and L2 not containing the origin.
The correct Answer is:A, B
To solve the problem, we need to analyze the given lines and determine the angle bisectors. Let's go through the solution step by step.
Step 1: Rewrite the equations of the lines
The lines are given as:
- L1:3x−4y+2=0
- L2:3y−4x−5=0
We can rewrite L2 in standard form:
4x−3y+5=0
Step 2: Identify coefficients
From the equations, we identify the coefficients:
- For L1: a1=3,b1=−4,c1=2
- For L2: a2=4,b2=−3,c2=5
Step 3: Calculate a1a2+b1b2
Now we calculate a1a2+b1b2:
a1a2+b1b2=(3)(4)+(−4)(−3)=12+12=24
Since 24>0, this indicates that the angle bisectors will be determined by the signs of the constants c1 and c2.
Step 4: Analyze the signs of c1 and c2
The constants are:
- c1=2 (positive)
- c2=5 (positive)
Since both constants are positive, we can conclude that:
- The acute angle bisector will contain the origin.
- The obtuse angle bisector will not contain the origin.
Step 5: Find the equations of the angle bisectors
The equations of the angle bisectors can be found using the formula:
a1x+b1y+c1√a21+b21=±a2x+b2y+c2√a22+b22
Calculating the denominators:
√a21+b21=√32+(−4)2=√9+16=5
√a22+b22=√42+(−3)2=√16+9=5
Step 6: Set up the equations
Thus, we have:
3x−4y+25=±4x−3y+55
Step 7: Solve for the acute angle bisector (positive sign)
Taking the positive sign:
3x−4y+2=4x−3y+5
Rearranging gives:
3x−4y+2−4x+3y−5=0⟹−x+y−3=0⟹x−y+3=0
Step 8: Solve for the obtuse angle bisector (negative sign)
Taking the negative sign:
3x−4y+2=−(4x−3y+5)
Rearranging gives:
3x−4y+2+4x−3y−5=0⟹7x−7y−3=0⟹x−y+1=0
Conclusion
The equations of the angle bisectors are:
1. For the acute angle bisector: x−y+3=0 (contains the origin)
2. For the obtuse angle bisector: x−y+1=0 (does not contain the origin)
Final Statements
- Statement (a) is incorrect.
- Statement (b) is correct.
- Statement (c) is incorrect.
- Statement (d) is correct.
The lines are given as:
- L1:3x−4y+2=0
- L2:3y−4x−5=0
4x−3y+5=0
From the equations, we identify the coefficients:
- For L1: a1=3,b1=−4,c1=2
- For L2: a2=4,b2=−3,c2=5
Now we calculate a1a2+b1b2:
a1a2+b1b2=(3)(4)+(−4)(−3)=12+12=24
Since 24>0, this indicates that the angle bisectors will be determined by the signs of the constants c1 and c2.
The constants are:
- c1=2 (positive)
- c2=5 (positive)
- The acute angle bisector will contain the origin.
- The obtuse angle bisector will not contain the origin.
The equations of the angle bisectors can be found using the formula:
a1x+b1y+c1√a21+b21=±a2x+b2y+c2√a22+b22
√a21+b21=√32+(−4)2=√9+16=5
√a22+b22=√42+(−3)2=√16+9=5
Thus, we have:
3x−4y+25=±4x−3y+55
Taking the positive sign:
3x−4y+2=4x−3y+5
Rearranging gives:
3x−4y+2−4x+3y−5=0⟹−x+y−3=0⟹x−y+3=0
Taking the negative sign:
3x−4y+2=−(4x−3y+5)
Rearranging gives:
3x−4y+2+4x−3y−5=0⟹7x−7y−3=0⟹x−y+1=0
The equations of the angle bisectors are:
1. For the acute angle bisector: x−y+3=0 (contains the origin)
2. For the obtuse angle bisector: x−y+1=0 (does not contain the origin)
- Statement (a) is incorrect.
- Statement (b) is correct.
- Statement (c) is incorrect.
- Statement (d) is correct.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MATRIX MATCH TYPE)8videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (SINGLE CORRECT ANSWER TYPE)82videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
The equation of the line which bisects the obtuse angle between the line x−2y+4=0 and 4x−3y+2=0 is
View SolutionFind the equations of the bisectors of the angles between the lines 12x+5y−4=0 and 3x+4y+7=0. Distinguish
the one which bisects the acute angle between the lines.View SolutionIf the point (a2,a+1) lies in the angle between the lines 3x−y+1=0 and x+2y−5=0 containing the origin, then find the value of a.
View SolutionIf the point (a2,a+1) lies in the angle between the lines 3x−y+1=0 and x+2y−5=0 containing the origin, then find the value of a.
View SolutionConsider the lines given by
L1:x+3y−5=0
L2:3x−ky−1=0
L3:5x+2y−12=0
Match the following lists.
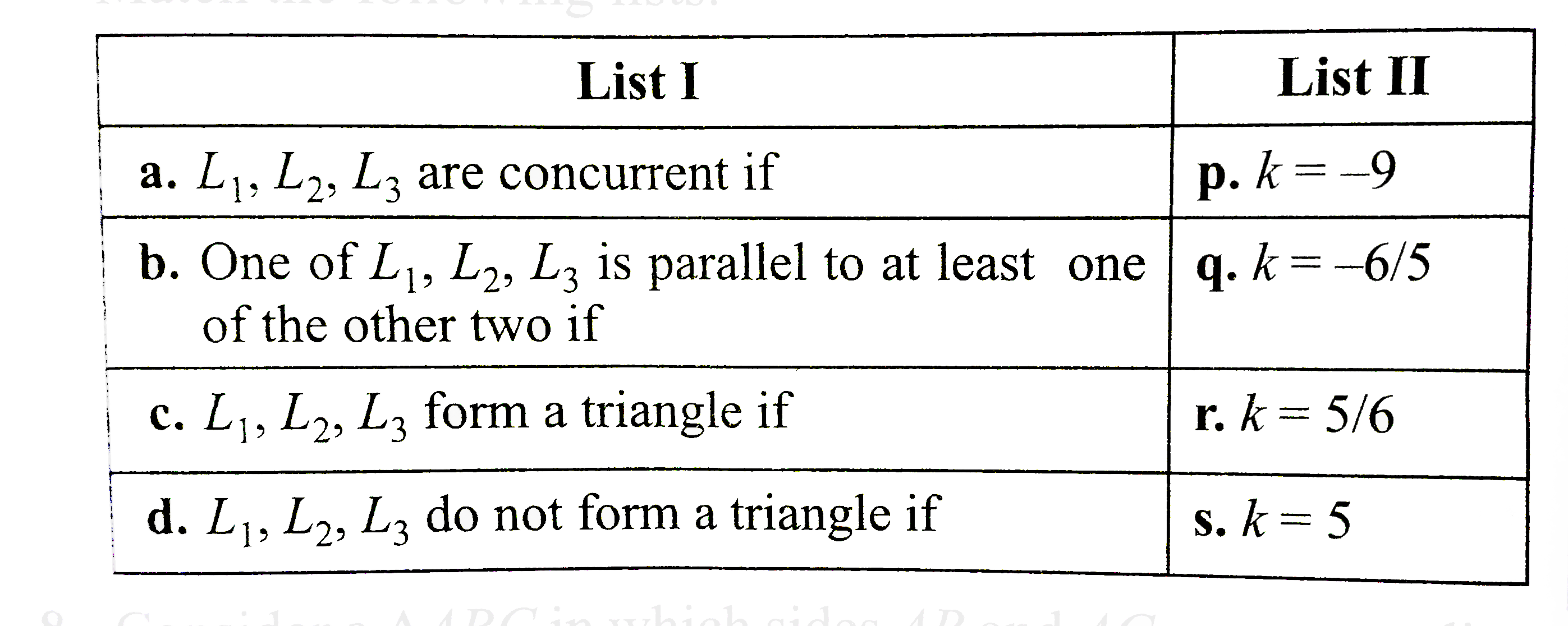 View Solution
View SolutionFind the equations of angular bisector bisecting the angle containing the origin and not containing the origin of the lines 4x+3y−6=0and5x+12y+9=0
View SolutionFind the equations of the lines bisecting the angles between the lines 4x−3y+12=0and12x+5y=20.
View SolutionTwo lines L1 and L2 of slops 1 are tangents to y2=4x and x2+2y2=4 respectively, such that the distance d units between L1andL2 is minimum, then the value of d is equal to
View SolutionFind the equation of the bisector of the obtuse angle between the lines 3x−4y+7=0 and 12x+5y−2=0.
View SolutionFind the equation of the bisector of the obtuse angle between the lines 3x−4y+7=0 and 12x+5y−2=0.
View Solution

