An electron in C5+ ion during the transition from n=3 to n=1 emits light of wavelength
2.85nm
3.6nm
8.7nm
9.8nm
The correct Answer is:A
To find the wavelength of light emitted during the transition of an electron in the C5+ ion from n=3 to n=1, we can use the Rydberg formula for hydrogen-like atoms:
1λ=Z2R(1n21−1n22)
Where:
- λ is the wavelength of emitted light,
- Z is the atomic number of the ion,
- R is the Rydberg constant (R≈1.097×107m−1),
- n1 is the lower energy level (1 in this case),
- n2 is the higher energy level (3 in this case).
1. Identify the values:
- For carbon (C), the atomic number Z=6.
- Transition from n2=3 to n1=1.
2. Substitute the values into the Rydberg formula:
1λ=62×1.097×107(112−132)
3. Calculate Z2:
Z2=62=36
4. Calculate the difference in the fractions:
112−132=1−19=1−0.1111=0.8889
5. Combine the results:
1λ=36×1.097×107×0.8889
6. Calculate 36×1.097×0.8889:
36×1.097≈39.492
39.492×0.8889≈35.104
7. Final calculation for 1λ:
1λ=35.104×107m−1
8. Calculate λ:
λ=135.104×107≈2.85×10−8m
9. Convert to nanometers:
λ≈2.85nm(since 1nm=10−9m)
Final Answer:
The wavelength of light emitted during the transition from n=3 to n=1 in the C5+ ion is approximately 2.85nm.
- λ is the wavelength of emitted light,
- Z is the atomic number of the ion,
- R is the Rydberg constant (R≈1.097×107m−1),
- n1 is the lower energy level (1 in this case),
- n2 is the higher energy level (3 in this case).
- For carbon (C), the atomic number Z=6.
- Transition from n2=3 to n1=1.
1λ=62×1.097×107(112−132)
Z2=62=36
112−132=1−19=1−0.1111=0.8889
1λ=36×1.097×107×0.8889
36×1.097≈39.492
39.492×0.8889≈35.104
1λ=35.104×107m−1
λ=135.104×107≈2.85×10−8m
λ≈2.85nm(since 1nm=10−9m)
The wavelength of light emitted during the transition from n=3 to n=1 in the C5+ ion is approximately 2.85nm.
Similar Questions
Knowledge Check
The ground state energy of an atom is −13.6eV. The photon emitted during the transition of electron from n=3 to n=1 state, is incidenet on a photosensitive material of unknown work function. The photoelectrons are emitted from the materials with a maximum kinetic energy of 9 eV. the threshold wavelength of the material used is
A0.9×10−7mB4×10−7mC0.47×10−7mD9×10−7m
The transition of electron from n = 3 to n = 1 in H atom produces
View SolutionAn electron in H atom makes a transition from n=3→n=1. The recoil momentum of the H atom will be
View SolutionAn electron in H atom makes a transition from n=3→n=1. The recoil momentum of the H atom will be
View SolutionAn electron in a hydrogen atom makes a transition from n1→n2. If the time period of electron in the initial state is eight times that in the final state then Find the ratio n1n2
View SolutionA photon of energy 10.2 eV corresponds to light of wavelength λ0. Due to an electron transition from n=2 to n=1 in a hydrogen atom, light of wavelength λ is emitted. If we take into account the recoil of the atom when the photon is emitted.
View SolutionCalculate the wavelength of radiation emited when an electron in a hydrogen atom makes a transition from an energy level with n=3 to a level with n=2
View SolutionIn a set of experiment on a hydrogen on a hypotherical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state (n=1) are shown in the energy level diagram
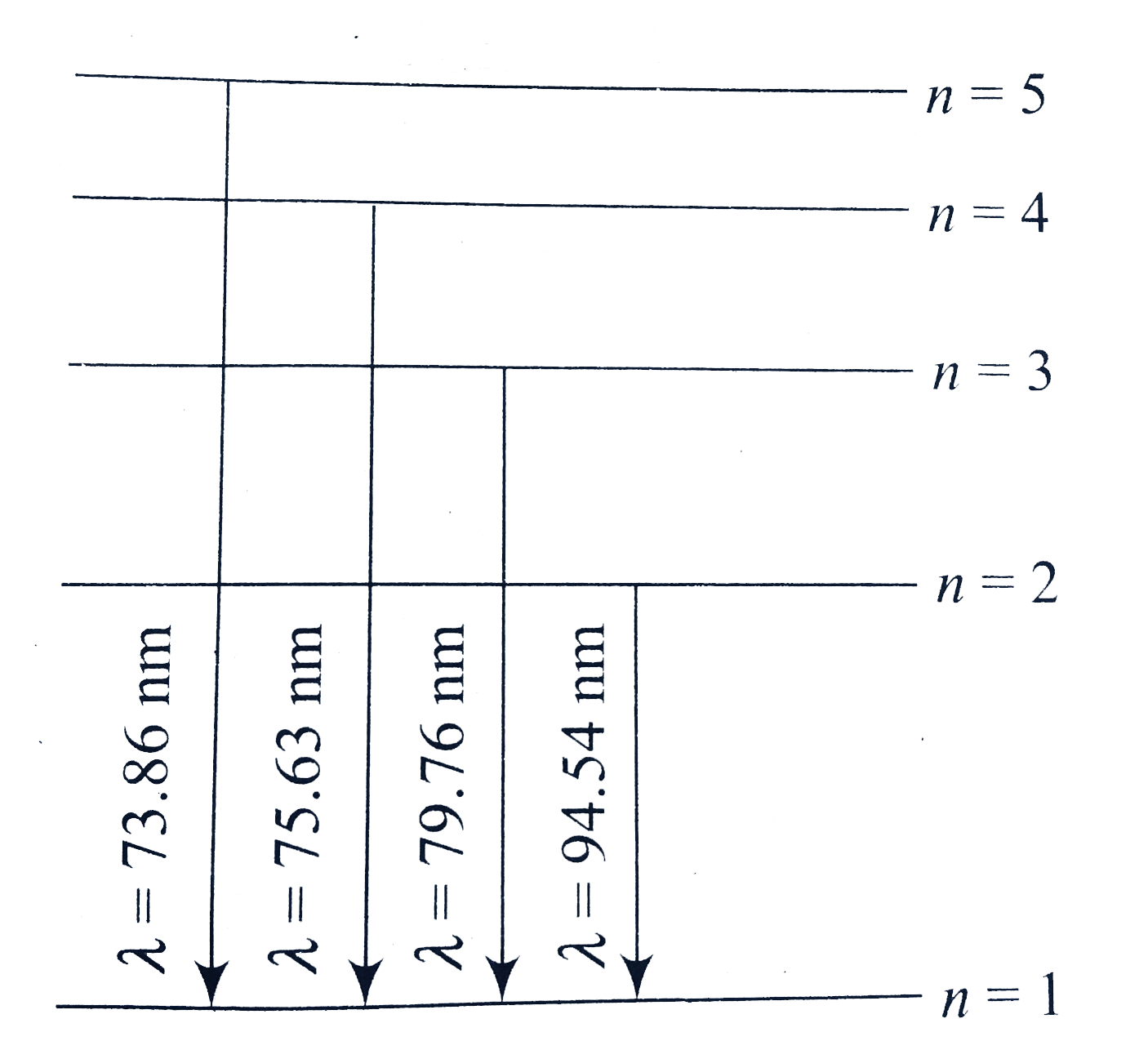
λ5→1=73.86nm
λ4→1=75.63nm
λ3→1=79.76nm
λ2→1=94.54nm
If an electron made a transition from n = 4 to n = 2 level, the wavelength of the light that it would emit is nearly
View Solution
