For the reaction , if mol , the value of would be
The correct Answer is:C
To solve the problem, we need to analyze the given reaction and apply the concept of reaction rates based on stoichiometry.
1. Write the balanced chemical equation:
N2+3H2→2NH3
2. Identify the stoichiometric coefficients:
- For N2, the coefficient is 1.
- For H2, the coefficient is 3.
- For NH3, the coefficient is 2.
3. Understand the relationship between the rates of change of concentrations:
The rate of the reaction can be expressed in terms of the change in concentration over time for each species involved:
−11d(N2)dt=−13d(H2)dt=12d(NH3)dt
4. Given information:
We know that:
d(NH3)dt=4×10−4mol L−1s−1
5. Relate the rate of formation of NH3 to the rate of disappearance of H2:
From the stoichiometry of the reaction, we can set up the following equation:
−13d(H2)dt=12d(NH3)dt
6. Substituting the known value of d(NH3)dt:
−13d(H2)dt=12×4×10−4
7. Calculate d(H2)dt:
−13d(H2)dt=2×10−4
Now, multiply both sides by -3 to solve for d(H2)dt:
d(H2)dt=−3×2×10−4=−6×10−4mol L−1s−1
8. Final answer:
The value of −d(H2)dt is:
6×10−4mol L−1s−1
N2+3H2→2NH3
- For N2, the coefficient is 1.
- For H2, the coefficient is 3.
- For NH3, the coefficient is 2.
The rate of the reaction can be expressed in terms of the change in concentration over time for each species involved:
−11d(N2)dt=−13d(H2)dt=12d(NH3)dt
We know that:
d(NH3)dt=4×10−4mol L−1s−1
From the stoichiometry of the reaction, we can set up the following equation:
−13d(H2)dt=12d(NH3)dt
−13d(H2)dt=12×4×10−4
−13d(H2)dt=2×10−4
Now, multiply both sides by -3 to solve for d(H2)dt:
d(H2)dt=−3×2×10−4=−6×10−4mol L−1s−1
The value of −d(H2)dt is:
6×10−4mol L−1s−1
Similar Questions
For the reaction , N2+3H2→2NH3 if d[NH3]dt=2×10−4mol L−1s−1 , the value of −d[H2]dt would be
View SolutionFor the reaction N2+3H2→2NH3 if
Δ[NH3]Δt=2×10−4molL−1s−1, the value of −Δ[H2]Δt would be
View SolutionFor the reaction N2(g)+3H2(g)→2NH3(g) if Δ[NH3]Δt=4×10−4mol.l−1s−1, the value of −Δ[H2]Δt would be
View SolutionN2+3H2→NH3
View SolutionN2+3H2→NH3
View SolutionA+2B→C+D. If −d[A]dt=5×10−4 mol L−1s−1, then −d[B]dt is :
View SolutionKp for the reaction N2+3H2⇔2NH3 at 400∘C is 1.64×10−4atm−2. Find Kc.
View SolutionIn the hober's process of ammonia manufacture,
N2(g)+3H2(g)→2NH3(g)
the rate of appearance of NH3 is :
d[NH3]dt=2×10−4molL−1sec−1
The rates of the reaction expressed in terms of N2andH2 will be :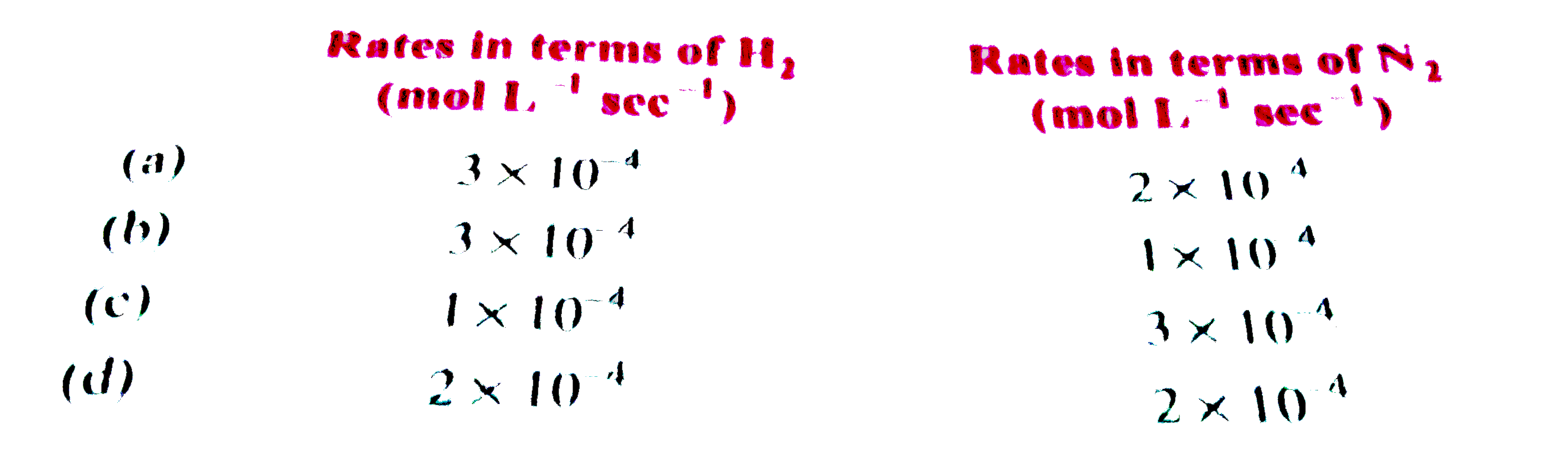
View SolutionFor the reaction
H2(g)+I2(g)→2HI(g), the rate of disappearance of H2 is 1.0×10−4molL−1s−1. The rate of appearance of HI will be
View SolutionIn a reaction N2(g)+3H2(g)→2NH3(g) rate of appearance of NH3 is 2.5×10−4molL−1sec−1 then rate of reaction and rate
of disappearance of H2 respectively is :-
View Solution
