A+2B→C+D. If −d[A]dt=5×10−4 mol L−1s−1, then −d[B]dt is :
2.5×10−4 mol L−1s−1
5.0×10−4 mol L−1s−1
2.5×10−3 mol L−1s−1
1.0×10−3 mol L−1s−1
The correct Answer is:D
To solve the problem, we need to analyze the given reaction and apply the concepts of chemical kinetics.
1. Understand the Reaction: The reaction is given as:
A+2B→C+D
This indicates that for every 1 mole of A that reacts, 2 moles of B are consumed.
2. Identify the Rate of Disappearance of A: We are given that the rate of disappearance of A is:
−d(A)dt=5×10−4mol L−1s−1
3. Relate the Rates of Disappearance: From the stoichiometry of the reaction, we can relate the rates of disappearance of A and B. The relationship can be expressed as:
−d(B)dt=21(−d(A)dt)
This means that for every mole of A that disappears, 2 moles of B disappear.
4. Substitute the Known Rate: Now, substituting the known rate of disappearance of A into the equation:
−d(B)dt=2(5×10−4)
5. Calculate the Rate of Disappearance of B:
−d(B)dt=10×10−4=1.0×10−3mol L−1s−1
6. Final Answer: Therefore, the rate of disappearance of B is:
−d(B)dt=1.0×10−3mol L−1s−1
A+2B→C+D
This indicates that for every 1 mole of A that reacts, 2 moles of B are consumed.
−d(A)dt=5×10−4mol L−1s−1
−d(B)dt=21(−d(A)dt)
This means that for every mole of A that disappears, 2 moles of B disappear.
−d(B)dt=2(5×10−4)
−d(B)dt=10×10−4=1.0×10−3mol L−1s−1
−d(B)dt=1.0×10−3mol L−1s−1
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - Level-2
50 Videos
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - Level-2 ( Numerical Value Type for JEE Main )
15 Videos
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - Level-0 (Long Answer Type )
6 Videos
- CHEMICAL EQUILIBRIUMBOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - IN-CHAPTER EXERCISE - G
10 Videos
- CHEMICAL THERMODYNAMICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - IN - CHAPTER EXERCISE - L
10 Videos
Similar Questions
For the reaction , N2+3H2→2NH3 if d[NH3]dt=2×10−4mol L−1s−1 , the value of −d[H2]dt would be
View SolutionFor the reaction N2+3H2→2NH3, if d[NH3]dt.=4×10−4 mol L−1s−1, the value of −d[H2]dt would be
View SolutionFor the reaction N2+3H2→2NH3, if d[NH3]dt.=4×10−4 mol L−1s−1, the value of −d[H2]dt would be
View SolutionIn the formation of sulphur trioxide by the contact process,
2SO2(g)+O2(g)⇔2SO3(g)
The rate of reaction is expressed as
−d(O2)dt=2.5×10−4molL−1s−1
The rate of disappearance of (SO2) will be
View SolutionIn the reaction , A+2B→6C+2D, if the initial rate −d[A]dt at t= 0 is 2.6×10−2Msec−1, what will be the value of −d[B]dt at t=0?
View SolutionThe rate of disappearance of A at two temperature is given by A⇔B
i. −d[A]dt=2×10−2[A]−4×10−3[B] at 300K
ii. −d[A]dt=4×10−2[A]−16×10−4[B] at 400K
From the given values of heat of reaction
View SolutionFor a reversible reaction
A+B⇔C
(dxdt)=2.0×103Lmol−1s−1[A][B]−1.0×102s−1[C] where x is the amount of 'A' dissociated. The value of equilibrium constant (Keq) is
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
A reaction follows the given concentration-time graph. The rate for this reaction at 20s will be
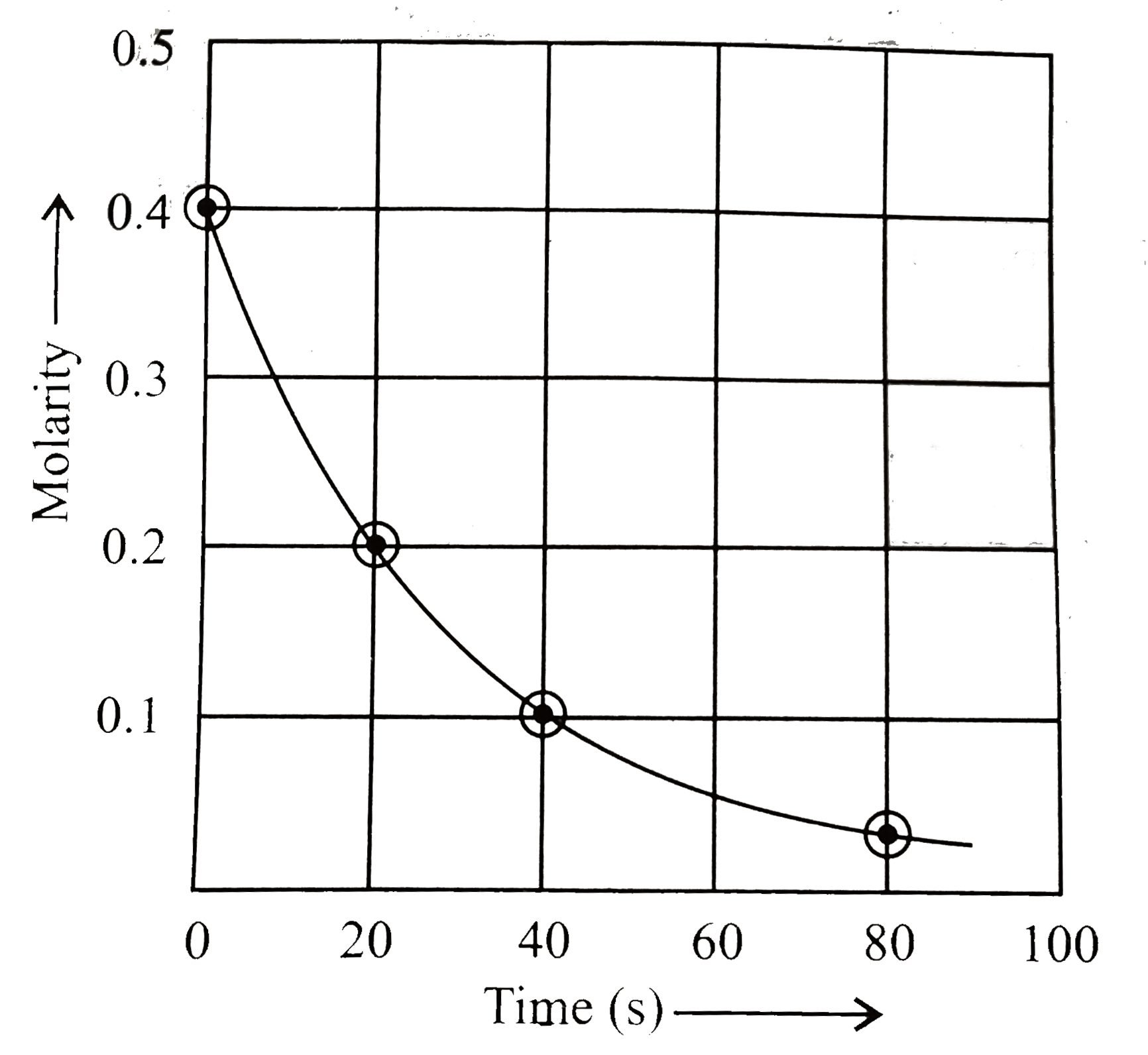
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
For reaction 3BrOɵ→BrOɵ3+2Brɵ, the value of rate constant at 80∘C in the rate law for −d[BrOɵ]dt was found to be 0.054Lmol−1s−1. The rate constant (k) for the reaction in terms of d[BrOɵ3]dt is
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
In the following reaction,
xA→yB
log.[−d[A]dt]=log.[d[B]dt]+0.3
where negative isgn indicates rate of disappearance of the reactant. Thus, x:y is:
View Solution