A 5kg mass bounces in simple harmonic motion at the end of a spring. At which point the acceleration of the mass is the greatest?
When the spring is fully compressed and when the spring is fully extended
When the spring is at its rest length
When the spring is halfway between its rest length and is fully extended or compressed length
The acceleration is constant.
The correct Answer is:A
To determine at which point the acceleration of a 5 kg mass bouncing in simple harmonic motion at the end of a spring is greatest, we can follow these steps:
1. Understanding Simple Harmonic Motion (SHM):
- In SHM, the restoring force acting on the mass is provided by the spring. This force is proportional to the displacement from the equilibrium position (rest length of the spring).
2. Spring Force:
- The force exerted by a spring is given by Hooke's Law:
F=−kx
where k is the spring constant and x is the displacement from the equilibrium position.
3. Acceleration in SHM:
- The acceleration a of the mass can be expressed as:
a=Fm=−kxm
Here, m is the mass of the object (5 kg in this case). The acceleration is directly proportional to the displacement x.
4. Maximum Displacement:
- The acceleration will be greatest when the displacement x is at its maximum value. This occurs when the spring is either fully compressed or fully extended.
5. Conclusion:
- Therefore, the points at which the mass experiences the greatest acceleration are when the spring is either fully compressed or fully extended. At these points, the displacement x is maximum, leading to maximum force and hence maximum acceleration.
Final Answer:
The acceleration of the mass is greatest when the spring is either fully compressed or fully extended.
- In SHM, the restoring force acting on the mass is provided by the spring. This force is proportional to the displacement from the equilibrium position (rest length of the spring).
- The force exerted by a spring is given by Hooke's Law:
F=−kx
where k is the spring constant and x is the displacement from the equilibrium position.
- The acceleration a of the mass can be expressed as:
a=Fm=−kxm
Here, m is the mass of the object (5 kg in this case). The acceleration is directly proportional to the displacement x.
- The acceleration will be greatest when the displacement x is at its maximum value. This occurs when the spring is either fully compressed or fully extended.
- Therefore, the points at which the mass experiences the greatest acceleration are when the spring is either fully compressed or fully extended. At these points, the displacement x is maximum, leading to maximum force and hence maximum acceleration.
The acceleration of the mass is greatest when the spring is either fully compressed or fully extended.
Similar Questions
A block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Find the maximum force exerted by the spring on the block.
View SolutionDerive an experession for the period of oscillation of a mass attached to a spring executing simple harmonic motion. Given that the period of oscillation depends on the mass m and the force constant k, where k is the force required to stretch the spring by unit length?
View Solution
Knowledge Check
A particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
A0.5πms−1,0ms−2B0.5ms−1,−5π2ms−2C0ms−1,−5π2ms−2D0.5πms−1,−0.5π2ms−2Assertion: Simple harmonic motion is the projection of uniform circular motion on the diameter of the circle in which the latter motion occurs.
Reason: Simple harmonic motion is a uniform motion.AIf both assertion and reson are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
For a particle executing simple harmonic motion, the acceleration is -
View SolutionConsider the graph shown for the position of a ball attached to a spring as it oscillates in simple harmonic motion. Which of the following is correct?
The speed of ball is greatest at 2s
(ii)The speed of ball is greatestat 4s
(iii)The acceleration of ball is greatest at 2s
(iv)The acceleration of ball is greatest at 6s
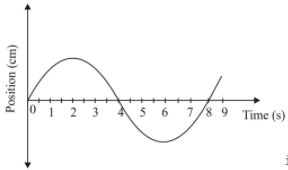
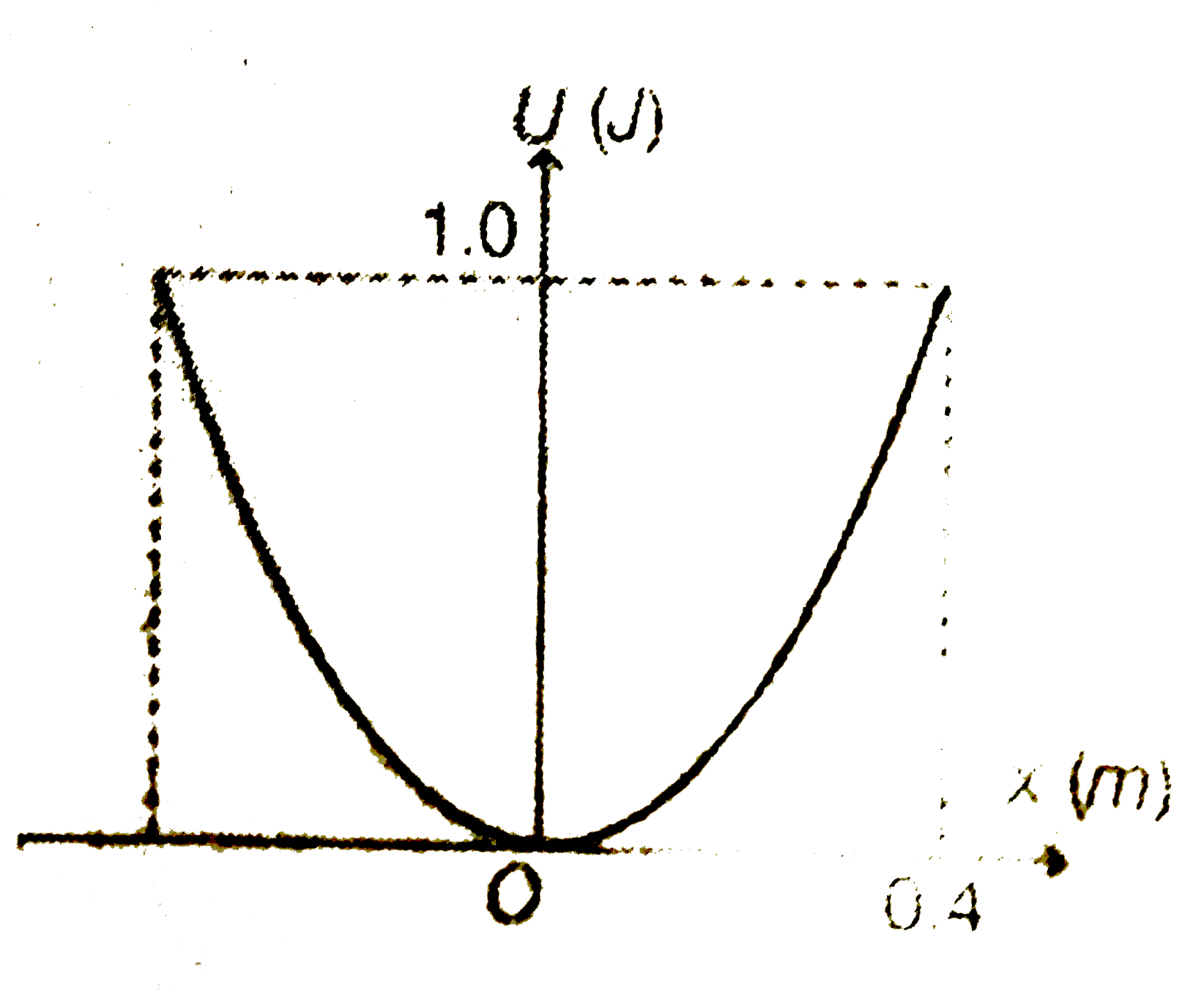
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
View SolutionAn object of mass 0.8kg is attached to one end of a spring and the system is set into simple harmonic motion. The displacement x of the object as a fuction of time is shown in the figure. With the aid of the data, determine
(a) the amplitude A of the motion,
(b) the angular frequency ω,
( c) the spring constant K,
(d) the speed of the object at t=1.0s and
(e) the magnitude of the object's acceleration at t=1.0s.

View Solution
