A particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
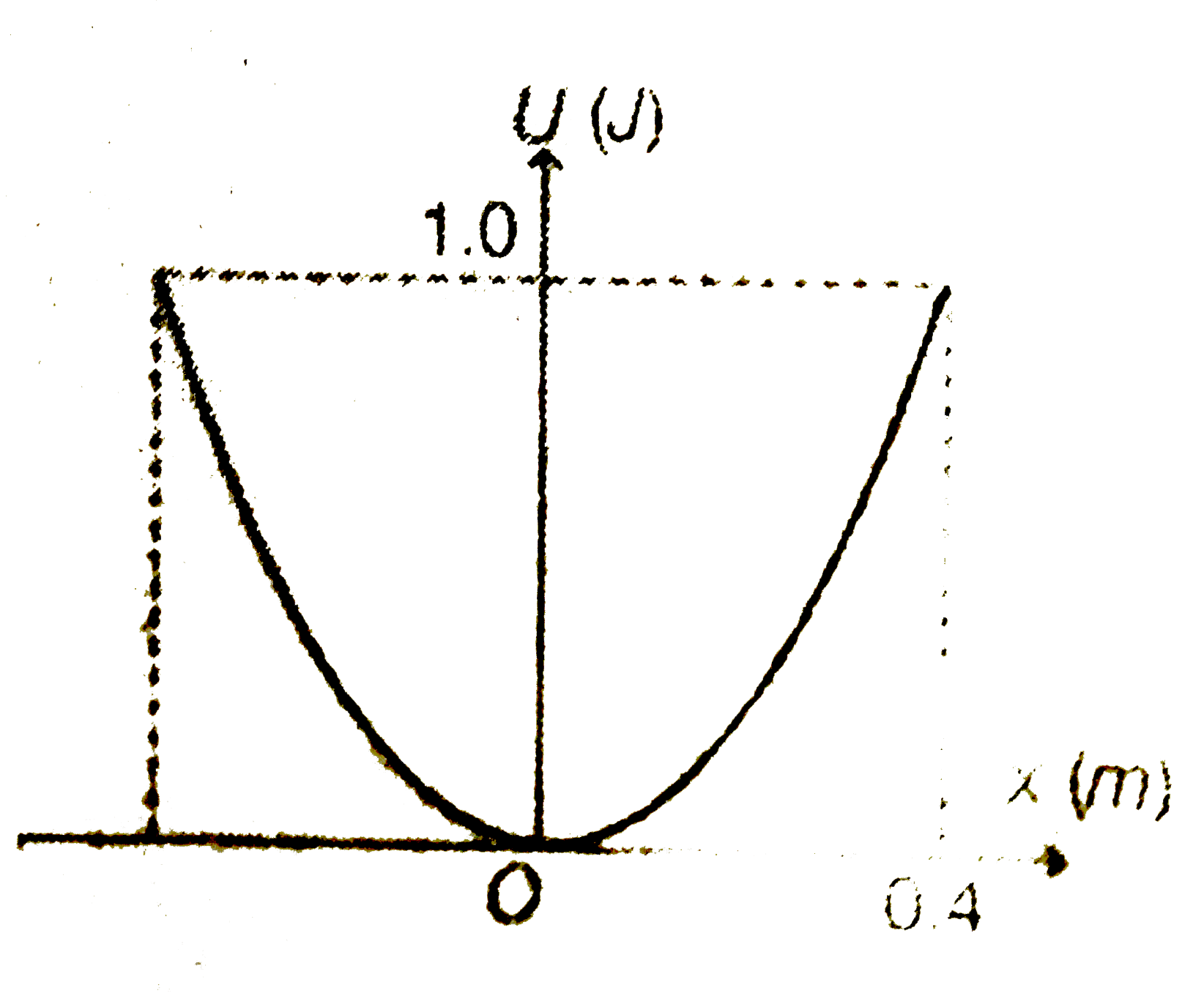
The correct Answer is:4
Step by step video & image solution for A particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is (npi)/5 second. Find value of n. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Matrix matching type questions
13 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View Solution
Knowledge Check
A particle is executing simple harmonic motion. Its total energy is proportional to its
Adisplacement from equilibrium positionBfrequency of oscillationCsquare of amplitude of motionDvelocity at equilibrium positionThe displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2π
A particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-
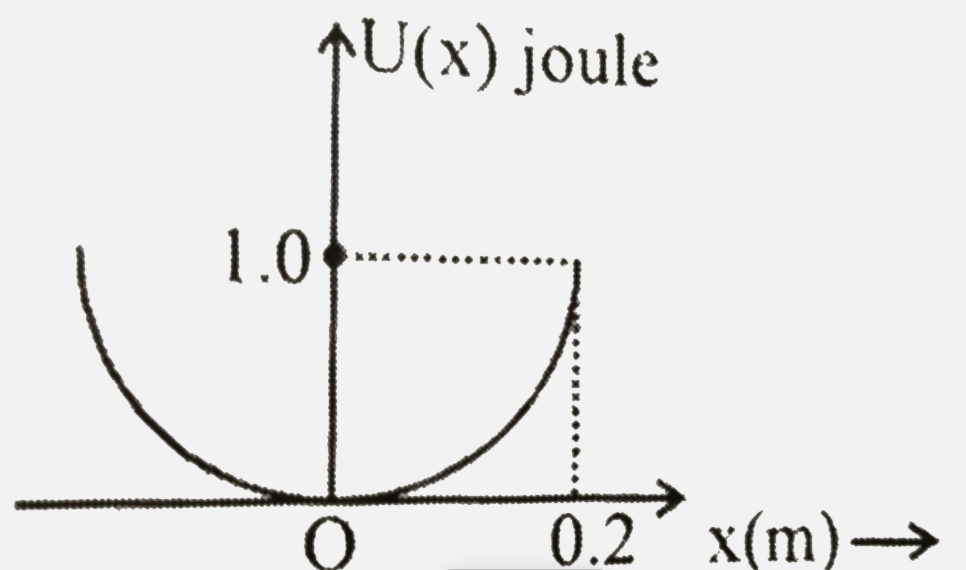
View SolutionThe variation of force (F) acting on a particle of mass 800 g with position (x) is as shown in figure. The time period of oscillation of the particles is
View SolutionA particle of mass 4 kg moves along x axis, potential energy ( U ) varies with respect to x as U=20+(x−4)2 , maximum speed of paritcle is at
View SolutionA particle of mass m moves in the potential energy U shoen above. The period of the motion when the particle has total energy E is
View SolutionA particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
View SolutionWhen a particle oscillates in simple harmonic motion, both in potential energy and kinetic energy vary sinusoidally with time. If v be the frequency of the motion of the particle, the frequency associated with the kinetic energy is :
View Solution
