Of the following, the equation of progressive wave is
y=Acosaxsinbt
y=Asinbt
y=Acos(ax+bt)
y=Atan(ax+bt)
The correct Answer is:C
To determine the equation of a progressive wave from the given options, we can analyze the characteristics of each equation provided.
1. Understanding Wave Types:
- A progressive wave is a wave that travels through space and time, characterized by a continuous change in phase.
- A standing wave, on the other hand, is formed by the interference of two waves traveling in opposite directions, resulting in nodes and antinodes.
2. Analyzing the First Equation:
- The first equation is identified as a standing wave equation. This is because, for any fixed position (x), the wave oscillates in time (t) but does not propagate through space. The amplitude varies with position, indicating it is not a progressive wave.
3. Analyzing the Second Equation:
- The second equation represents simple harmonic motion (SHM) but does not include both x and t in a way that indicates propagation. Each particle oscillates with a different amplitude, which suggests it is also not a progressive wave.
4. Analyzing the Third Equation:
- The third equation includes a term that combines both x and t, typically in the form of (t ± x/v). This indicates that the wave is moving through space, which is characteristic of a progressive wave. The presence of both variables in this manner suggests that it describes a wave traveling in a specific direction.
5. Analyzing the Fourth Equation:
- Similar to the third equation, the fourth equation also includes both x and t in a manner that suggests propagation. It can be expressed in the form of (t ± x/v), confirming it as a progressive wave.
6. Conclusion:
- Based on the analysis, the equations that represent progressive waves are the third and fourth equations. They both include the necessary variables and format that indicate a wave traveling through space and time.
Final Answer:
The equations of progressive waves are the third and fourth equations.
- A progressive wave is a wave that travels through space and time, characterized by a continuous change in phase.
- A standing wave, on the other hand, is formed by the interference of two waves traveling in opposite directions, resulting in nodes and antinodes.
- The first equation is identified as a standing wave equation. This is because, for any fixed position (x), the wave oscillates in time (t) but does not propagate through space. The amplitude varies with position, indicating it is not a progressive wave.
- The second equation represents simple harmonic motion (SHM) but does not include both x and t in a way that indicates propagation. Each particle oscillates with a different amplitude, which suggests it is also not a progressive wave.
- The third equation includes a term that combines both x and t, typically in the form of (t ± x/v). This indicates that the wave is moving through space, which is characteristic of a progressive wave. The presence of both variables in this manner suggests that it describes a wave traveling in a specific direction.
- Similar to the third equation, the fourth equation also includes both x and t in a manner that suggests propagation. It can be expressed in the form of (t ± x/v), confirming it as a progressive wave.
- Based on the analysis, the equations that represent progressive waves are the third and fourth equations. They both include the necessary variables and format that indicate a wave traveling through space and time.
The equations of progressive waves are the third and fourth equations.
Similar Questions
Shows the shape of a progressive wave at time t=0. after a time t=(1)/(80), the particle at the origin has its maximum negative displacement.if the wave speed is 80 units maximum negative displacement. If the wave speed is 80 units, then find the equation of the progressive wave.
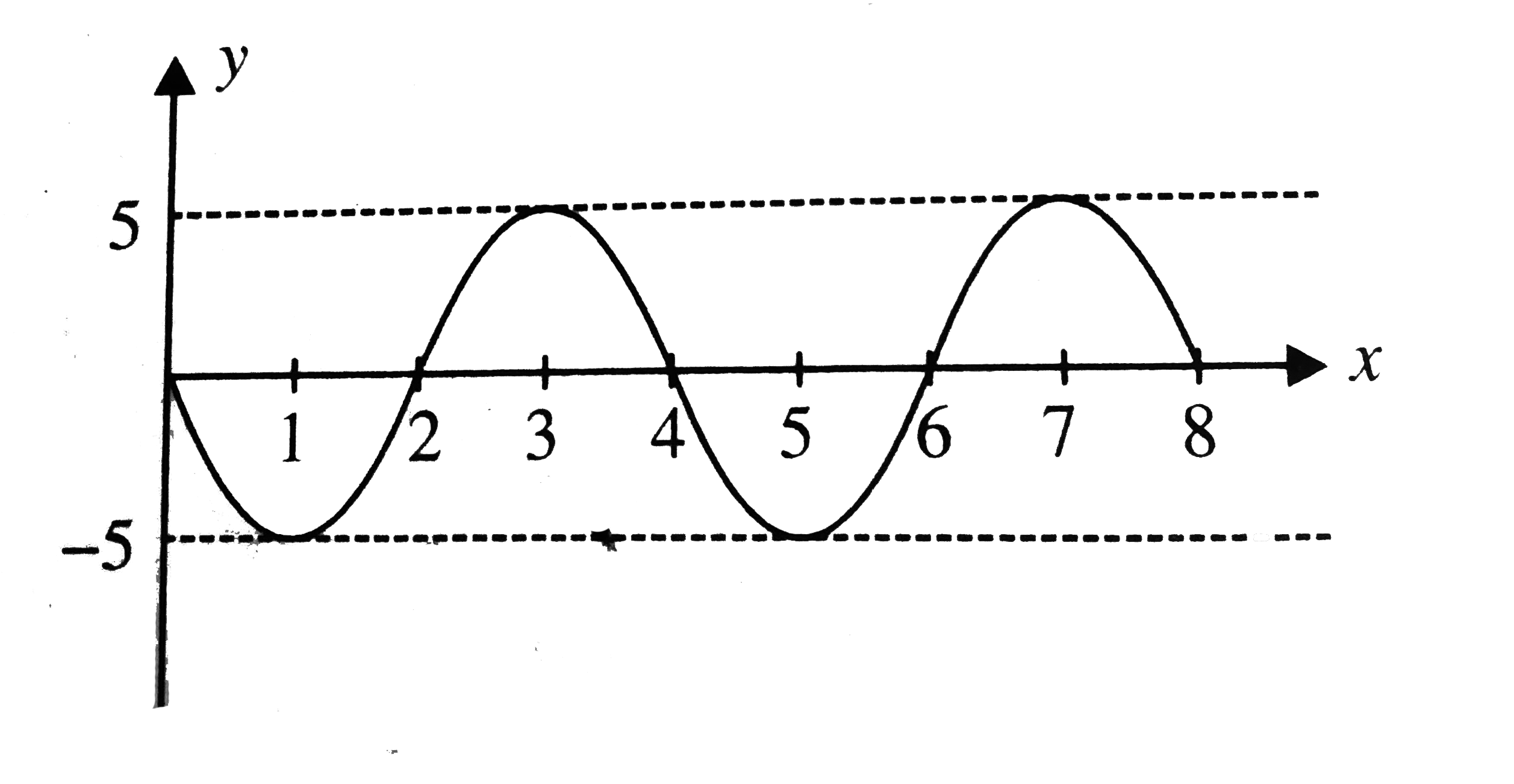 .
.
View SolutionWrite down the equation of progressive wave travelling along the negative X-axis and having an amplitude of 0.21m frequency of 225 Hz nd a wavelength of 0.6 m.
View SolutionA progressive wave of frequency 500 Hz is travelling with a velocity of 360 m/s. How far apart are two points 60∘ out of phase ?
(ii)Does the speed of a plane-progressive wave depend on the amplitude ?
(iii)The equation of a progressive wave is represented by Y=Asin2(kx−ωt). Find its amplitude and frequency
(iv)Which of the following equations represents a wave travelling along positive y-axis ? (a)x=5 sin (2y-6t) (b) y=6sin (7x-5t) (c ) y=10 sin (6y) cos (8t)
View SolutionThe following equations represent progressive transverse waves
z1=Acos(ωt−kx)
z2=Acos(ωt+kx)
z3=Acos(ωt+ky)
z4=Acos(2ωt−2ky)
A stationary wave will be formed by superposing
View SolutionIf the equation of progressive wave is given by y=4sinπ[t5−x9+π6] then, which of the following is correct ? (Assume SI units )
View Solution(b) Write the equation of a progressive wave propagating along the positive x-direction, whose amplitude is 5 cm, frequency 250 Hz and velocity 500ms−1.
View SolutionWhich of the following equations represents as wave travelling along Y-axis?
View SolutionWhich of the following equations represent a transverse wave travelling along- y axis ?
View SolutionWhich of the following equation reprsents a wave ?
View SolutionWrite down the differential equation of a plane progressive wave.
View Solution
