A particle tied to a string describes a vertical circular motion of radius r continually. If it has a velocity √3gr at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is
1:6
1:4
1:3
1:2
The correct Answer is:B
To solve the problem, we need to find the ratio of the tensions in the string at the highest and lowest points of a vertical circular motion of a particle.
1. Identify Forces at the Highest Point:
At the highest point of the circular motion, the forces acting on the particle are:
- The gravitational force (weight) acting downward: mg
- The tension in the string TH acting downward
- The centripetal force required for circular motion: mv2Hr
The equation for the forces at the highest point can be written as:
TH+mg=mv2Hr
2. Substituting the Given Velocity:
We are given that the velocity at the highest point vH=√3gr. Substituting this into the equation gives:
TH+mg=m(√3gr)2r
TH+mg=m(3gr)r
TH+mg=3mg
Rearranging this gives:
TH=3mg−mg=2mg
3. Identify Forces at the Lowest Point:
At the lowest point of the circular motion, the forces acting on the particle are:
- The gravitational force (weight) acting downward: mg
- The tension in the string TL acting upward
- The centripetal force required for circular motion: mv2Lr
The equation for the forces at the lowest point can be written as:
TL−mg=mv2Lr
4. Finding Velocity at the Lowest Point Using Energy Conservation:
Using conservation of mechanical energy between the highest and lowest points:
12mv2H+mg(2r)=12mv2L+mg(0)
Substituting vH=√3gr:
12m(3gr)+2mgr=12mv2L
3mgr2+2mgr=12mv2L
3mgr+4mgr2=12mv2L
7mgr2=12mv2L
Canceling 12m gives:
v2L=7gr
5. Substituting Back to Find Tension at the Lowest Point:
Now substituting v2L=7gr into the tension equation at the lowest point:
TL−mg=m(7gr)r
TL−mg=7mg
Rearranging gives:
TL=7mg+mg=8mg
6. Finding the Ratio of Tensions:
Now we can find the ratio of the tensions at the highest and lowest points:
Ratio=THTL=2mg8mg=28=14
Final Answer:
The ratio of the respective tensions in the string at the highest and lowest points is 1:4.
At the highest point of the circular motion, the forces acting on the particle are:
- The gravitational force (weight) acting downward: mg
- The tension in the string TH acting downward
- The centripetal force required for circular motion: mv2Hr
TH+mg=mv2Hr
We are given that the velocity at the highest point vH=√3gr. Substituting this into the equation gives:
TH+mg=m(√3gr)2r
TH+mg=m(3gr)r
TH+mg=3mg
Rearranging this gives:
TH=3mg−mg=2mg
At the lowest point of the circular motion, the forces acting on the particle are:
- The gravitational force (weight) acting downward: mg
- The tension in the string TL acting upward
- The centripetal force required for circular motion: mv2Lr
TL−mg=mv2Lr
Using conservation of mechanical energy between the highest and lowest points:
12mv2H+mg(2r)=12mv2L+mg(0)
Substituting vH=√3gr:
12m(3gr)+2mgr=12mv2L
3mgr2+2mgr=12mv2L
3mgr+4mgr2=12mv2L
7mgr2=12mv2L
Canceling 12m gives:
v2L=7gr
Now substituting v2L=7gr into the tension equation at the lowest point:
TL−mg=m(7gr)r
TL−mg=7mg
Rearranging gives:
TL=7mg+mg=8mg
Now we can find the ratio of the tensions at the highest and lowest points:
Ratio=THTL=2mg8mg=28=14
The ratio of the respective tensions in the string at the highest and lowest points is 1:4.
Similar Questions
A particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v0 to complete the vertical circle. The tension in the string when it becomes horizontal is
View SolutionA particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
View Solution
Knowledge Check
The ride is circus rides along a circular track in a vertical plane. The minimum velocity at the highest point of the track will be
A√(2gR)B√(5gR)C√(3gR)D√(gR)
A fighter plane is moving in a vertical circle of radius 'r'. Its minimum velocity at the highest point of the circle will be
View SolutionA particle tied to a string moves in a circular path in vertical plane. Its velocity at lowerst point is such that it just completes circle. Find the ratio of resultant force on particle at the lowerst point to that at highest point.
View SolutionA stone is fastened to one end of a string and is whirled in a verticla circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
View SolutionA stone of mass 1kg is tied with a string and it is whirled in a vertical circle of radius 1 m. If tension at the highest point is 14 N, then velocity at lowest point will be
View SolutionA heavy particle of weight w, attached to a fixed point by a light inextensible string describes a circle in a vertical plane. The tension in the string has the values nw and mw respectively when the particle is at the highest and lowest points in the path. Then :
View SolutionA body is moving in a vertical circle of radius r such that the string is just taut at its highest point. The speed of the particle when the string is horizontal is
View SolutionFigure shows a smooth vertical circular track AB of radius R. A block slides along the surface AB when it is given a velocity equal to √6gR at point A. The ratio of the force exerted by the track on the block at point A to that at point B is
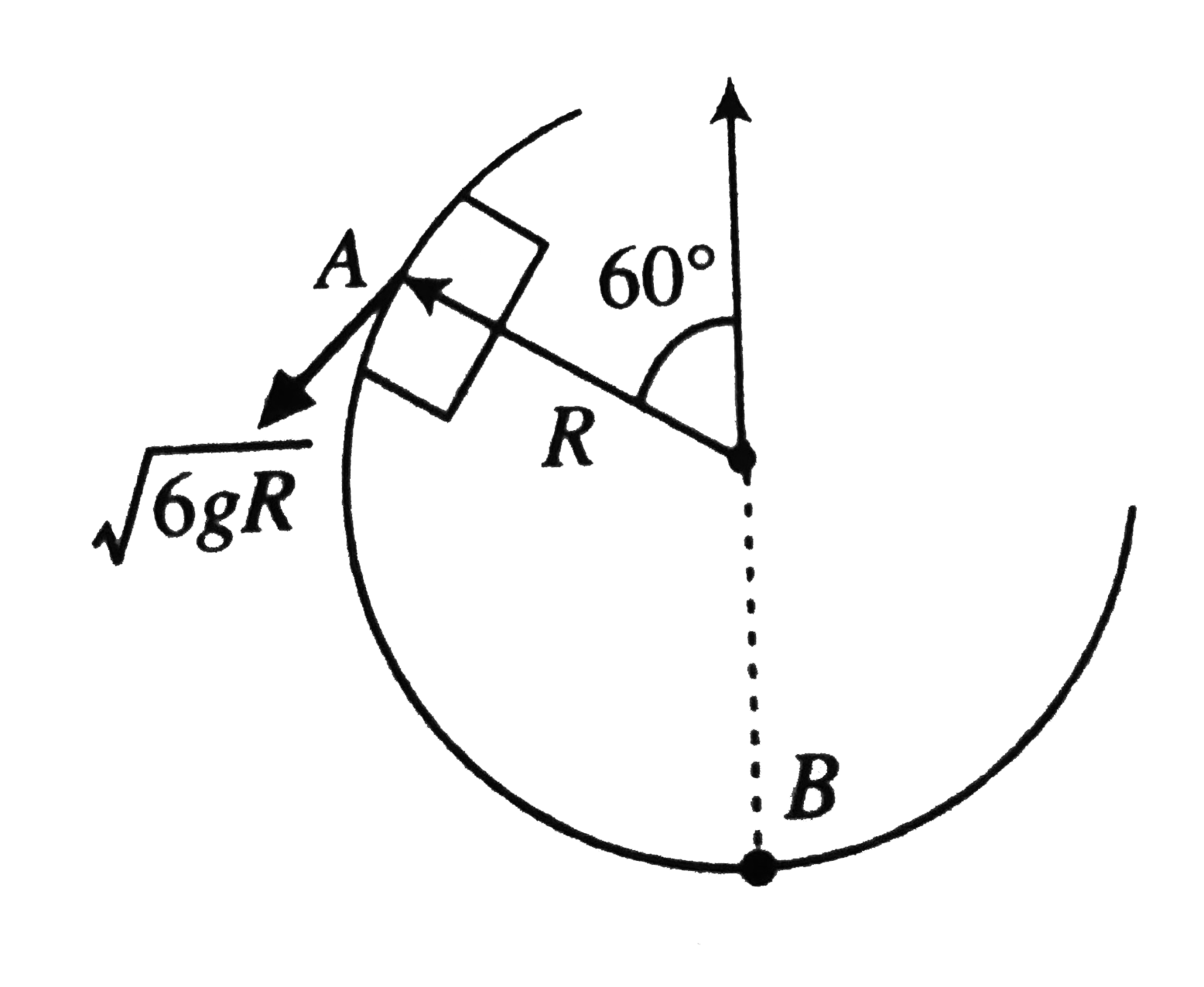
View Solution
