In △ABC, D is a point on side BC such that ∠ADC=∠BAC. If CA = 12 cm, CB = 8 cm, then CD is equal to:
त्रिभुज ABC में भुजा BC पर D बिंदु इस प्रकार स्थित है कि ∠ADC=∠BAC होता है। यदि CA = 12 सेमी, CB = 8 सेमी, तो CD निम्नलिखित में किसके बराबर है?
15
12
18
16
To solve the problem, we will use the properties of similar triangles.
1. Understand the Given Information:
- We have triangle ABC.
- D is a point on side BC such that ∠ADC = ∠BAC.
- CA = 12 cm and CB = 8 cm.
- We need to find the length of CD.
2. Identify the Similar Triangles:
- Since ∠ADC = ∠BAC, triangles ADC and ABC are similar by the Angle-Angle (AA) criterion for similarity of triangles.
3. Set Up the Proportions:
- From the similarity of triangles, we can write the proportion:
CDCB=CAAB
- Let CD = x. Then, CB = 8 cm and CA = 12 cm.
4. Express AB in Terms of CD:
- We can express AB in terms of the segments on BC. Since D divides BC into two segments, we have:
AB=CB+CD=8+x
5. Substituting into the Proportion:
- Substitute the known values into the proportion:
x8=128+x
6. Cross-Multiply:
- Cross-multiplying gives us:
x(8+x)=12⋅8
- This simplifies to:
x2+8x=96
7. Rearranging the Equation:
- Rearranging gives us a quadratic equation:
x2+8x−96=0
8. Solving the Quadratic Equation:
- We can use the quadratic formula x=−b±√b2−4ac2a where a=1,b=8,c=−96:
x=−8±√82−4⋅1⋅(−96)2⋅1
x=−8±√64+3842
x=−8±√4482
x=−8±8√72
x=−4±4√7
9. Finding the Positive Solution:
- Since CD cannot be negative, we take the positive solution:
CD=−4+4√7
10. Calculating the Value:
- Approximating √7≈2.64575:
CD≈−4+4⋅2.64575≈−4+10.583=6.583 cm
Final Answer:
Thus, the length of CD is approximately 6.58 cm.
- We have triangle ABC.
- D is a point on side BC such that ∠ADC = ∠BAC.
- CA = 12 cm and CB = 8 cm.
- We need to find the length of CD.
- Since ∠ADC = ∠BAC, triangles ADC and ABC are similar by the Angle-Angle (AA) criterion for similarity of triangles.
- From the similarity of triangles, we can write the proportion:
CDCB=CAAB
- Let CD = x. Then, CB = 8 cm and CA = 12 cm.
- We can express AB in terms of the segments on BC. Since D divides BC into two segments, we have:
AB=CB+CD=8+x
- Substitute the known values into the proportion:
x8=128+x
- Cross-multiplying gives us:
x(8+x)=12⋅8
- This simplifies to:
x2+8x=96
- Rearranging gives us a quadratic equation:
x2+8x−96=0
- We can use the quadratic formula x=−b±√b2−4ac2a where a=1,b=8,c=−96:
x=−8±√82−4⋅1⋅(−96)2⋅1
x=−8±√64+3842
x=−8±√4482
x=−8±8√72
x=−4±4√7
- Since CD cannot be negative, we take the positive solution:
CD=−4+4√7
- Approximating √7≈2.64575:
CD≈−4+4⋅2.64575≈−4+10.583=6.583 cm
Thus, the length of CD is approximately 6.58 cm.
Topper's Solved these Questions
Similar Questions
In △ABC ,D is a point on side BC such that ∠ADC=∠BAC. If CA = 12 cm, and CB = 8cm, then CD is equal to :
त्रिभुज ABC में, D भुजा BC पर स्थित एक बिंदु है जो इस प्रकार है कि ∠ADC=∠BAC है |यदि CA = 12 सेमी और CB = 8 सेमी है, तो CD का मान किसके बराबर होगा ?
View SolutionIn a △ABC, D is a point on side BC such that ∠ADC=∠BAC. If CA = 12 cm, CB = 8cm, then CD is equal to: △ABC में , D, भुजा BC पर एक बिंदु है इस प्रकार है कि ∠ADC=∠BAC यदि CA = 12 सेमी, CB = 8 सेमी, तो CD बराबर है: (wrong Question)
View Solution
Knowledge Check
In ΔABC, D is a point on side BC such that ∠ADC=∠BAC, If CA = 12 cm, CB = 8 cm then CD is equal to :
A18 cmB12 cmC16 cmD15 cmD is a point on the side BC of △ABC such that ∠ADC=∠BAC. If CA = 12 cm and BC = 16 cm, then the length of CD is :
A12 cmB6 cmC8 cmD9 cm
In △ABC ,D and E are the points on sides AC and AB, respectively, such that ∠ADE=∠B. If AE = 8 cm, CD = 3 cm, DE= 6 cm and BC = 9 cm, then AD is equal to:
त्रिभुज ABC में, D तथा E क्रमश भुजा AC और AB पर स्थित बिंदु है जो इस प्रकार है कि ∠ADE=∠B है| यदि AE = 8 सेमी, CD = 3 सेमी, DE = 6 सेमी और BC = 9 सेमी है, तो AD का मान किसके बराबर है ?
View SolutionIn △ABC ,∠A=90∘. M is the midpoint of BC and D is a point on BC such that AD⊥BC. If AB= 7 cm and AC = 24 cm, then AD:AM is equal to:
△ABC में, ∠A=90∘ है, M, BC का मध्य बिंदु है तथा D, BC पर स्थित ऐसा बिंदु है कि AD⊥BC है | यदि AB= 7 सेमी, AC = 24 सेमी है, तो AD:AM किसके बराबर है ?
View SolutionIn △ABC ,D and E are the points on sides AC and AB, respectively, such that ∠ADE=∠B. If AD = 7.6 cm, AE = 7.2 cm, BE = 4.2 cm and BC = 8.4 cm, then DE is equal to:
त्रिभुज ABC में, D तथा E भुजा AC और AB पर स्थित ऐसे बिंदु ∠ADE=∠B है| यदि AD =7.6 सेमी, AE = 7.2 सेमी, BE = 4.2 सेमी तथा BC = 8.4 सेमी है, तो DE किसके बराबर है ?
View SolutionIn the given figure , D is a point on the side BC of ΔABC such that ∠ADC=∠BAC. Prove that CA2=CB×CD.
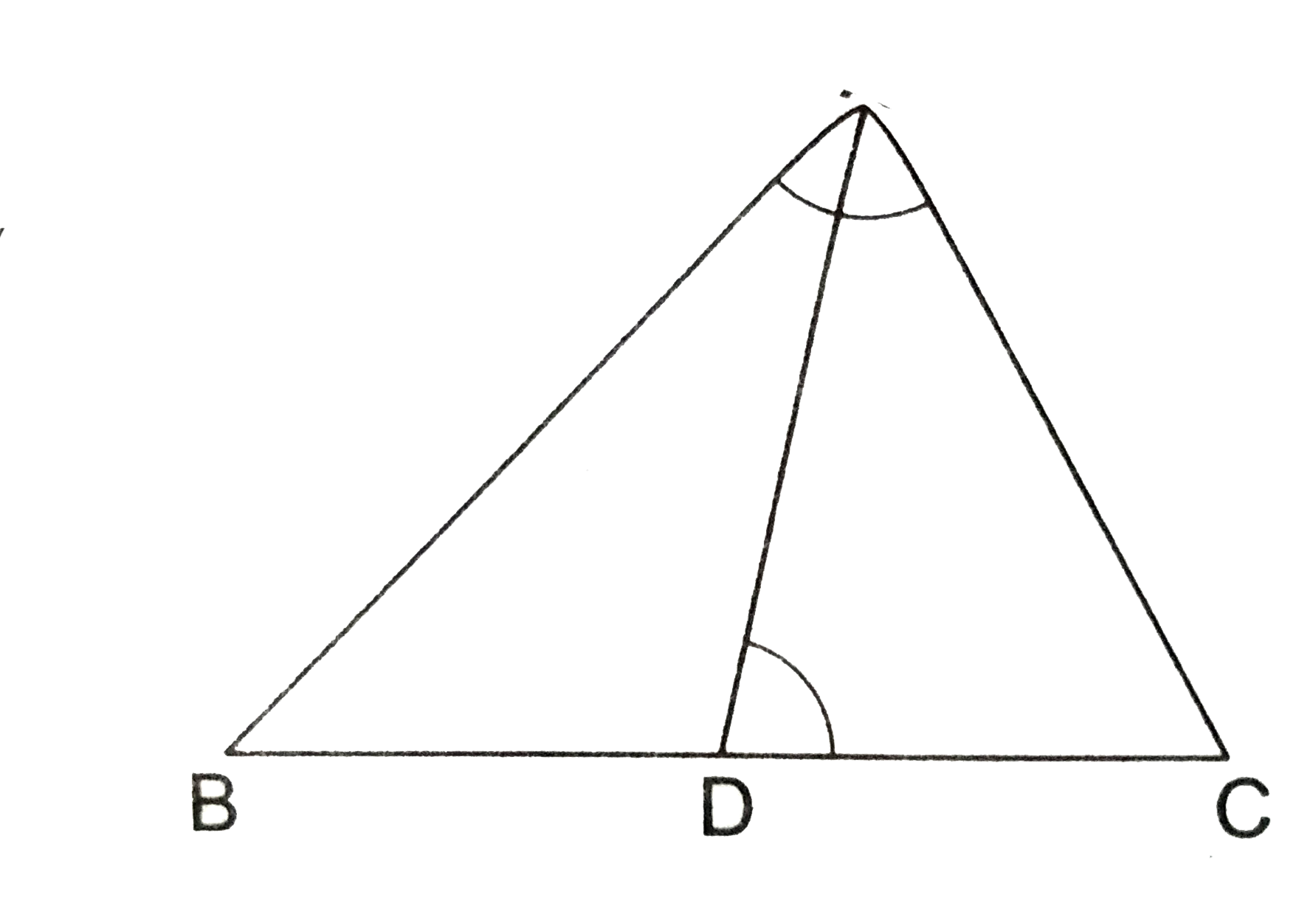
View SolutionIn △ABC,D is a point on BC such that AD is the bisector of ∠A, AB = 11.7 cm, AC = 7.8 cm and BC = 13 cm. What is the length (in cm) of DC?
त्रिभुज ABC में, D, BC पर स्थित एक ऐसा बिंदु है कि AD, ∠A का समद्विभाजक है |AB =11.7 सेमी, AC = 7.8 सेमी तथा BC =13 सेमी है | DC की लंबाई ( सेमी में ) कितनी है?
View SolutionIn △ADC, E and B are the points on the sides AD and AC respectively such that ∠ABE=∠ADC. If AE = 6cm, BC = 2cm, BE = 3cm and CD = 5cm, then (AB + DE) is :
त्रिभुज ADC में, E और D क्रमशः भुजाओं AD और AC पर स्थित ऐसे बिंदु हैं कि ∠ABE=∠ADC है | यदि AE = 6 सेमी, BC = 2 सेमी तथा BE =3 सेमी और CD = 5 सेमी है, तो (AB + DE) का मान ज्ञात करें|
View Solution
