A right circular cylinder has height 28cm and radius of base 14cm. Two hemispheres of
radius 7 cm each are cut from each of the two bases of the cylinder. What is the total
surface area (in cm2) of the remaining part?
a) 3842
b) 4312
c) 3296
d) 4436
To find the total surface area of the remaining part of the right circular cylinder after cutting out two hemispheres from each base, we can follow these steps:
Step 1: Calculate the Surface Area of the Cylinder
The formula for the total surface area (TSA) of a cylinder is given by:
TSA=2πr(h+r)
Where:
- r is the radius of the base of the cylinder.
- h is the height of the cylinder.
Given:
- Height h=28 cm
- Radius r=14 cm
Substituting the values into the formula:
TSA=2π(14)(28+14)
=2π(14)(42)
=2π(588)
=1176π cm2
Step 2: Calculate the Surface Area of the Hemispheres
The surface area of one hemisphere is given by:
Surface Area of Hemisphere=2πr2
For two hemispheres, the total surface area is:
Total Surface Area of Hemispheres=2×2πr2=4πr2
Given the radius of the hemispheres r=7 cm:
Total Surface Area of Hemispheres=4π(72)
=4π(49)
=196π cm2
Step 3: Calculate the Total Surface Area of the Remaining Part
After cutting out the hemispheres, we need to subtract the area of the hemispheres from the total surface area of the cylinder and add the area of the circular edges created by the hemispheres.
The area of the circular edges created by the hemispheres is equal to the area of the circular bases of the hemispheres, which is:
Area of Circular Edges=2×πr2=2×π(72)=2×π(49)=98π cm2
Now, we can find the total surface area of the remaining part:
Total Surface Area of Remaining Part=TSA of Cylinder−TSA of Hemispheres+Area of Circular Edges
Substituting the values:
=1176π−196π+98π
=(1176−196+98)π
=1078π cm2
Step 4: Calculate the Numerical Value
Using π≈227:
1078π≈1078×227≈1078×3.14≈3381.32 cm2
Thus, rounding to the nearest whole number, the total surface area of the remaining part is approximately:
≈3381 cm2
Final Answer
The total surface area of the remaining part is 3381 cm2.
---
The formula for the total surface area (TSA) of a cylinder is given by:
- r is the radius of the base of the cylinder.
- h is the height of the cylinder.
- Height h=28 cm
- Radius r=14 cm
=2π(14)(42)
=2π(588)
=1176π cm2
The surface area of one hemisphere is given by:
=4π(49)
=196π cm2
After cutting out the hemispheres, we need to subtract the area of the hemispheres from the total surface area of the cylinder and add the area of the circular edges created by the hemispheres.
=(1176−196+98)π
=1078π cm2
Using π≈227:
The total surface area of the remaining part is 3381 cm2.
Topper's Solved these Questions
Similar Questions
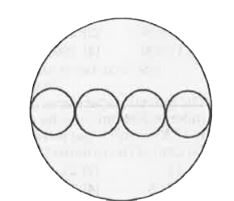
A solid cylinder has radius of base 14 cm and height 15 cm, 4 identical cylinder are cut from each base as shown in the given figure. Height of small cylinder is 5 cm. What is the total surface area (in cm2) of the remaining part ?
View SolutionFrom a right circular cylinder with height 10cm and radius of base 6cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid.
View Solution
Knowledge Check
A right circular solid cylinder has radius of base 7 cm and height is 28 cm. It is melted to form a cuboid such that the ratio of its side is 2 : 3 : 6. What is the total surface area (incm2) cuboid ?
A72x(1078)23B36x(2078)23C72x(2078)23D36x(1078)23A right circular cylinder has height as 18 cm and radius as 7 cm. The cylinder is cut in three equal parts (by 2 cuts parallel to base). What is the percentage increase in total surface area?
A62B56C48D52The volume of a right circular cylinder, 14 cm in height is equal to that of a cube whose edge is 11 cm. The radius of the base of the cylinder is (a) 5.2 cm (b) 5.5 cm (c) 11 cm (d) 22 cm
A5.2 cmB5.5 cmC11 cmD22 cm
A conical hole is drilled in a circular cylinder of height 12 cm and base radius 5 cm. The height and the base radius of the cone are also the same. Find the whole surface and volume of the remaining cylinder.
View SolutionA cone of same height and same base radius is cut from a cylinder of height 8 cm and base radius 6 cm .Find the total surface area and volume of the remaining solid.
View SolutionFrom a solid cylinder of height 4cm and radius 3cm a conical cavity of height 4cm of base radius 3cm is hollowed out. What is the total surface area of the remaining solid?
View SolutionA solid cylinder having radius of base as 7 cm. and length as 20 cm is bisected from its height to get two identical cylinders. What will be the percentage increase in the total surface area ?
View SolutionA solid cylinder having radius of base as 7 cm. and length as 20 cm is bisected from its height to get two identical cylinders. What will be the percentage increase in the total surface area ?
View Solution
