Two spheres of equal radius are taken out by cutting from a solid cube of side (12+4√3) cm. What is the maximum volume (in cm3)
of each sphere?
समान त्रिज्या वाले दो गोले को एक ठोस घन जिसकी भुजा (12+4√3) से.मी. है, से काट कर निकाला गया है।, प्रत्येक गोले का अधि कतम आयतन (से.मी.3 में) क्या है?
1077.31
905.14
966.07
1007.24
To find the maximum volume of each sphere that can be cut from a solid cube with a side length of (12+4√3) cm, we will follow these steps:
Step 1: Identify the side length of the cube
The side length of the cube A is given as:
A=12+4√3 cm
Step 2: Calculate the diagonal of the cube
The diagonal d of the cube can be calculated using the formula:
d=A√3
Substituting the value of A:
d=(12+4√3)√3
Step 3: Set up the equation for the radius of the spheres
Since we are cutting out two spheres of equal radius r, the total diameter of the two spheres must equal the diagonal of the cube:
d=2r√3
Thus, we can write:
(12+4√3)√3=2r√3
Step 4: Simplify the equation
Dividing both sides by √3:
12+4√3=2r
Now, solving for r:
r=12+4√32=6+2√3
Step 5: Calculate the volume of each sphere
The volume V of a sphere is given by the formula:
V=43πr3
Substituting the value of r:
V=43π(6+2√3)3
Step 6: Expand (6+2√3)3
To calculate (6+2√3)3:
(6+2√3)3=63+3⋅62⋅(2√3)+3⋅6⋅(2√3)2+(2√3)3
Calculating each term:
- 63=216
- 3⋅62⋅(2√3)=3⋅36⋅2√3=216√3
- 3⋅6⋅(2√3)2=3⋅6⋅12=216
- (2√3)3=8⋅3√3=24√3
Combining these:
(6+2√3)3=216+216+(216√3+24√3)=432+240√3
Step 7: Substitute back into the volume formula
Now substituting back into the volume formula:
V=43π(432+240√3)
Step 8: Calculate the final volume
Calculating the volume:
V=43⋅π⋅432+43⋅π⋅240√3
This gives the maximum volume of each sphere.
Final Answer
The maximum volume of each sphere is approximately:
V≈905.14 cm3
The side length of the cube A is given as:
A=12+4√3 cm
The diagonal d of the cube can be calculated using the formula:
d=A√3
Substituting the value of A:
d=(12+4√3)√3
Since we are cutting out two spheres of equal radius r, the total diameter of the two spheres must equal the diagonal of the cube:
d=2r√3
Thus, we can write:
(12+4√3)√3=2r√3
Dividing both sides by √3:
12+4√3=2r
Now, solving for r:
r=12+4√32=6+2√3
The volume V of a sphere is given by the formula:
V=43πr3
Substituting the value of r:
V=43π(6+2√3)3
To calculate (6+2√3)3:
(6+2√3)3=63+3⋅62⋅(2√3)+3⋅6⋅(2√3)2+(2√3)3
Calculating each term:
- 63=216
- 3⋅62⋅(2√3)=3⋅36⋅2√3=216√3
- 3⋅6⋅(2√3)2=3⋅6⋅12=216
- (2√3)3=8⋅3√3=24√3
(6+2√3)3=216+216+(216√3+24√3)=432+240√3
Now substituting back into the volume formula:
V=43π(432+240√3)
Calculating the volume:
V=43⋅π⋅432+43⋅π⋅240√3
This gives the maximum volume of each sphere.
The maximum volume of each sphere is approximately:
V≈905.14 cm3
Topper's Solved these Questions
Similar Questions
A sphere of radius 21 cm is cut into 8 identical parts by 3 cuts (1 cut along each axis). What will be the total surface area (in cm2) of each part?
एक 21 से.मी. त्रिज्या वाले गोले को 3 कटाव (प्रत्येक अक्ष पर 1 कयव) लगाकर 8 समरूप भागों में काटा जाता है। प्रत्येक भाग का कुल पृष्ठीय क्षेत्रफल (से.मी.2 में) क्या होगा?
View SolutionA right triangular prism has equilateral triangle as its base. Side of the triangle is 15 cm. Height of the prism is 20√3 cm. What is the volume (in cm3) of the prism?
एक लम्बवत त्रिभुजाकार प्रिज्म का आधार समबाहु त्रिभुज है। त्रिभुज को भुजा 15 से.मी. है। प्रिज्म की ऊँचाई 20√3से.मी. है। प्रिज्म का आयतन (से.मी.2 में) क्या है?
View Solution"A solid cube has side 8 cm. It is cut along diagonals) of top face to get 4 equal parts.What is the total surface area (in cm2) of each part?
एक ठोस घन की भुजा 8 से.मी. हैं वह ऊपर सतह के विकर्णों पर 4 समान भागों में काय जाता है। प्रत्येक भाग का कूल पृष्ठीय क्षेत्रफल (से.मी.2 में) क्या है?
View SolutionIf the radius of a sphere is increased by 4 cm, its surface area is increased by 464πcm2. What is the volume (in cm3) of the original sphere ?
यदि किसी गोले की त्रिज्या 4 सेमी से बढ़ा दी जाए, तो इसका पृष्ठ क्षेत्रफल 464π वर्ग सेमी से बढ़ जाता है | आरंभिक गोले का आयतन ( घन सेमी में ) क्या था ?
View SolutionTwo identical hemispheres of maximum possible size are cut from a solid cube of side 14cm. The bases of the hemispheres are part ofthe two oppoiste faces of cube. What is the total volume (in cm3) of the remainging part of the cube?
दो समरूप अधिकतम संभव माप वाले अर्धगालों को एक 14 से.मी. भुजा वाले ठोस घन से काटा ज़ाता हैं अर्धगोलों के आधार घन के दो विपरीत फलक के भाग है। घन के शेष भाग का कुल आयतन (से.मी.3 में) क्या है?
View SolutionThe base of a right prism is a regular hexagon of side 5 cm. If its height is 12√3 cm, then its volume (in cm3) is:
एक प्रिज्म का आधार 5 सेमी का एक नियमित षटभुज है। यदि इसकी ऊंचाई 12√3 सेमी है, तो इसकी आयतन (cm3 में ) है
View SolutionA regular pyramid has a square base. The height of the pyramid is 22 cm and side of its base is 14 cm. Volume of pyramid is equal to the volume of a sphere. What is the radius (in cm) of the sphere?
एक सम पिरामिड का आधार एक वर्ग है। पिरामिड को ऊँचाई 22 से.मी. है तथा उसके आधार की भुजा 14 से.मी. है। पिरामिड का आयतन एक गोले के आयतन के बराबर हैं गोले की त्रिज्या (से.मी. में) क्या है?
View SolutionThe base of a prism is in the shape of an equilateral triangle. If the perimeter of the base is 18 cm and the height of the prism is 20 cm, then what is the volume (in cm3) of the prism?
एक प्रिज्म का आधार समबाहु त्रिभुज के आकार में है। यदि आधार की परिधि 18 से.मी. है तथा प्रिज्म को ऊँचाई 20 से.मी. है, तो प्रिज्म का आयतन (से.मी.3 में) क्या हैं?
View SolutionA regular hexagonal base prism has height 8 cm and side of base is 4cm. What is the total surface area (in cm2) of the prism?
एक सम षट्भुज आधार वाले प्रिज्म की ऊँचाई 8 से.मी. है तथा आधार को भुजा 4 से.मी. है। प्रिज्म का कुल पृष्ठीय क्षेत्रफल (से.मी.2 में) क्या है?
View SolutionIn the given figure, PQR is an equilateral triangle with side as 12cm. S and T are the mid points of the sides PQ and PR respectively. What is the area (in cm2) of the shaded region?
दी गई आकृति में PQR एक समबाहु त्रिभुज है जिसकी भुजा 12 से.मी. हैं। S तथा T क्रमशः भुजा PQ तथा PR के मध्य बिन्दु है। छायांकित भाग का क्षेत्रफल (से.मी.2 में) क्या है?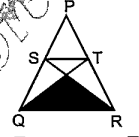
View Solution
