Two identical hemispheres of maximum possible size are cut from a solid cube of side 14cm. The bases of the hemispheres are part ofthe two oppoiste faces of cube. What is the total volume (in cm3) of the remainging part of the cube?
दो समरूप अधिकतम संभव माप वाले अर्धगालों
को एक 14 से.मी. भुजा वाले ठोस घन से काटा ज़ाता हैं अर्धगोलों के आधार घन के दो विपरीत फलक के भाग है। घन के शेष भाग का कुल आयतन (से.मी.3 में) क्या है?
1556.33
898.5
1467.33
1306.67
To solve the problem, we need to find the total volume of the remaining part of the cube after cutting out two identical hemispheres. Let's go through the steps one by one.
Step 1: Calculate the Volume of the Cube
The volume V of a cube is given by the formula:
V=a3
where a is the length of the side of the cube.
Given that the side of the cube is 14 cm:
V=143=14×14×14=2744cm3
Step 2: Determine the Radius of the Hemispheres
Since the hemispheres are cut from the cube and are of maximum possible size, the diameter of each hemisphere is equal to the side of the cube. Therefore, the radius r of each hemisphere is:
r=142=7cm
Step 3: Calculate the Volume of One Hemisphere
The volume Vh of a hemisphere is given by the formula:
Vh=23πr3
Substituting r=7cm:
Vh=23π(7)3=23π(343)=6863πcm3
Using π≈227:
Vh=6863×227=686×2221=1519221cm3
Step 4: Calculate the Volume of Two Hemispheres
Since there are two identical hemispheres, the total volume Vtotal_h of the two hemispheres is:
Vtotal_h=2×Vh=2×6863π=13723πcm3
Substituting π:
Vtotal_h=1372×2221=3028421cm3
Step 5: Calculate the Remaining Volume of the Cube
The remaining volume Vremaining of the cube after removing the volume of the two hemispheres is:
Vremaining=Vcube−Vtotal_h
Substituting the values:
Vremaining=2744−1372×2221
Calculating 1372×2221:
=3028421≈1441.14cm3
Now, subtracting:
Vremaining=2744−1441.14≈1302.86cm3
Final Answer
The total volume of the remaining part of the cube is approximately:
≈1302.86cm3
The volume V of a cube is given by the formula:
V=a3
where a is the length of the side of the cube.
V=143=14×14×14=2744cm3
Since the hemispheres are cut from the cube and are of maximum possible size, the diameter of each hemisphere is equal to the side of the cube. Therefore, the radius r of each hemisphere is:
r=142=7cm
The volume Vh of a hemisphere is given by the formula:
Vh=23πr3
Substituting r=7cm:
Vh=23π(7)3=23π(343)=6863πcm3
Using π≈227:
Vh=6863×227=686×2221=1519221cm3
Since there are two identical hemispheres, the total volume Vtotal_h of the two hemispheres is:
Vtotal_h=2×Vh=2×6863π=13723πcm3
Substituting π:
Vtotal_h=1372×2221=3028421cm3
The remaining volume Vremaining of the cube after removing the volume of the two hemispheres is:
Vremaining=Vcube−Vtotal_h
Substituting the values:
Vremaining=2744−1372×2221
Calculating 1372×2221:
=3028421≈1441.14cm3
Now, subtracting:
Vremaining=2744−1441.14≈1302.86cm3
The total volume of the remaining part of the cube is approximately:
≈1302.86cm3
Topper's Solved these Questions
Similar Questions
How many three digit numbers are there in which all the digits are odd?
तीन अंको वाली ऐसी कितनी संख्याएँ हैं जिसमें सभी अंक विषम है?
View SolutionThe given pie chart shows the breakup of total number of the employees of a company working in different offices (A, B, C, D and E). Total No. of employees = 2400
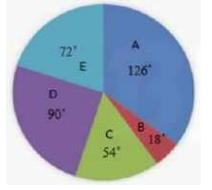 If the percentage of male employees in office C is 20% and that of female employees in E is 40%, then what is the ratio of the number of female employees in C to that of female employees in E?
If the percentage of male employees in office C is 20% and that of female employees in E is 40%, then what is the ratio of the number of female employees in C to that of female employees in E?
View SolutionA cube is placed inside a cone of radius 20cm and height 10cm, one of its face being on the base of the cone and vertices of opposite face touching the cone. What is the length (in cm) of side of the cube? एक घन को एक शंकु जिसकी त्रिज्या 20 से. मी. तथा ऊँचाई 10 से.मी. है, के अंदर रखा जाता है, उसको एक सतह शंकु के आधार कौर ओर है तथा विपरीत सतह के शीर्ष शंकु का स्पर्श कर रहे है। घन की भुजा लम्बाई (से. मी. में) क्या है ?
View SolutionTwo spheres of equal radius are taken out by cutting from a solid cube of side (12+4√3) cm. What is the maximum volume (in cm3) of each sphere?
समान त्रिज्या वाले दो गोले को एक ठोस घन जिसकी भुजा (12+4√3) से.मी. है, से काट कर निकाला गया है।, प्रत्येक गोले का अधि कतम आयतन (से.मी.3 में) क्या है?
View SolutionIdentical cubes of largest possible size are cut from a solid cuboid of size 65 cm x 26 cm x 3.9 cm. What is the total surface area (in cm2) of all the small cubes taken together?
एक ठोस घनाभ जिसका मान 65 से.मी. x 26 से.मी. x 3.9 से.मी. है, से अधिकतम संभव माप वाले समरूप घनों को काटा गया। सभी छोटे घनों को मिलाकर कूल पृष्ठीय क्षेत्रफल (से.मी.2 में) क्या है?
View SolutionA pyramid has a square base. The side of square is 12 cm and height of pyramid is 21 cm. The pyramid is cut into 3 parts by 2 cuts parallel to its base. The cuts are at height of 7 cm and 14 cm respectively from the base. What is the difference (in cm3) in the volume of top most and bottom most part?
एक पिरामिड का आधार एक वर्ग है। वर्ग की भुजा 12 से.मी. तथा पिसमिड की ऊँचाई 21 से.मी. है। पिरामिड को उसके आधार के समांतर 2 कर्टावों से 3 भागों में काटा जाता है। कटाव आधार से. क्रमशः 7 से.मी. तथा 14 से.मी. को ऊँचाई पर है। सबसे ऊपर तथा सबसे नीचे के भाग के आयतन का अंतर (से.मी.3 में)क्या हैं।
View SolutionA solid cube of volume 13824cm3 is cut into 8 cubes of equal volumes. The ratio of the surface area of the original cube to the sum of the surface areas of three of the smaller cubes is :
13824 घन सेमी आयतन वाले एक ठोस घन को बराबर आयतन वाले आठ घनों में काटा जाता है| आरंभिक घन के पृष्ठ क्षेत्रफल तथा तीन छोटे घनों के पृष्ठ क्षेत्रफलों के योग का अनुपात क्या है ?
View SolutionA cube of side 1 m length is cut into small cubes of side 10 cm each. How many such small cubes can be obtained?
1 मी लंबी भुजा वाले किसी घन को 10 सेमी भुजा वाले प्रत्येक छोटे-छोटे घनों में काटा जाता है | ऐसे कितने छोटे घन प्राप्त किये जा सकते हैं ?
View SolutionA right circular cylinder of maximum possible size is cut out from a solid wooden cube. The remaining material of the cube is what percentage of the original cube? (Take π= 3.14)
View SolutionA solid cube is cut into three cuboids of same volumes. What is the ratio of the surface area of the cube to the sum of the surface areas of any two of the cuboids so formed ?
एक ठोस घन को समान आयतन वाले तीन घनाभों में काटा जाता है | घन के पृष्ठ क्षेत्रफल तथा किसी भी दो घनाभ के पृष्ठ क्षेत्रफलों के जोड़ के बीच अनुपात ज्ञात करें |
View SolutionA sphere of maximum volume is cut out from a solid hemisphere. What is the ratio of the volume of the sphere to that of the remaining solid ?
किसी ठोस अर्धगोले से अधिकतम आयतन वाला एक गोला काटा जाता है | गोले के आयतन एवं शेष बचे ठोस के आयतन के बीच अनुपात ज्ञात करें |
View SolutionThe side of a cube is 15cm. What is the base area of a cuboid whose volume is 175cm3 less than that of the cube and whose height is 32 cm?
एक घन की भुजा 15 सेमी है | उस घनाभ के आधार का क्षेत्रफल ज्ञात करें जिसका आयतन घन के आयतन से 175 घन सेमी कम है तथा जिसकी ऊंचाई 32 सेमी है |
View SolutionThe volume of a cube is 216 cm^3 . What is the area of one face of the cube? किसी घन का आयतन 216 cm^3 है | इस घन के एक फलक का क्षेत्रफल ज्ञात करें |
View SolutionHow many cubes with a side 10 cm can be cut out of a cube having a side of 10 metre ?
10 मीटर भुजा वाले एक घन से 10 सेमी भुजा वाले कितने घन काटे जा सकते हैं ?
View SolutionFrom a spherical solid made of wood with radius 6 cm, a cube of maximum possible volume is cut. The side of the cube is : लकड़ी के बने 6 cm त्रिज्या के एक ठोस से, अधिकतम संभावित परिमाण (वॉल्यूम) के एक घन को हटाया जाता है | घन की भुजा ज्ञात कीजिये|
View Solution
