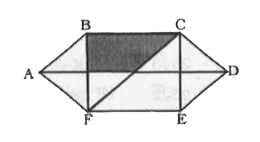
ABCDEF is a regular hexagon of side 12cm. What is the area (in cm2) of the triangle ECD?
ABCDEF 12 से.मी. भुजा वाला एक सम षट्भुज है। त्रिभुज ECD का क्षेत्रफल (से.मी.2 में) क्या है?
18√3
24√3
36√3
42√3
To find the area of triangle ECD in a regular hexagon ABCDEF with a side length of 12 cm, we can follow these steps:
Step 1: Understand the Geometry of the Hexagon
A regular hexagon can be divided into 6 equilateral triangles. Each internal angle of a regular hexagon is 120 degrees.
Step 2: Identify the Vertices of Triangle ECD
In the hexagon ABCDEF:
- E is the vertex at the bottom left,
- C is the vertex at the top right,
- D is the vertex directly below C.
Step 3: Determine the Lengths of the Sides
Since ABCDEF is a regular hexagon with each side measuring 12 cm:
- The length of EC = 12 cm (side of the hexagon)
- The length of CD = 12 cm (side of the hexagon)
Step 4: Calculate the Area of Triangle ECD
The area of a triangle can be calculated using the formula:
Area=12×a×b×sin(θ)
where a and b are the lengths of two sides, and θ is the angle between them.
For triangle ECD:
- a=EC=12cm
- b=CD=12cm
- θ=120∘
Step 5: Substitute Values into the Area Formula
Substituting the values into the area formula:
Area=12×12×12×sin(120∘)
Step 6: Calculate sin(120∘)
Using the sine value:
sin(120∘)=sin(180∘−60∘)=sin(60∘)=√32
Step 7: Complete the Area Calculation
Now substituting sin(120∘) back into the area formula:
Area=12×12×12×√32
=12×144×√32
=144√34
=36√3cm2
Final Answer
The area of triangle ECD is 36√3cm2.
---
A regular hexagon can be divided into 6 equilateral triangles. Each internal angle of a regular hexagon is 120 degrees.
In the hexagon ABCDEF:
- E is the vertex at the bottom left,
- C is the vertex at the top right,
- D is the vertex directly below C.
Since ABCDEF is a regular hexagon with each side measuring 12 cm:
- The length of EC = 12 cm (side of the hexagon)
- The length of CD = 12 cm (side of the hexagon)
The area of a triangle can be calculated using the formula:
Area=12×a×b×sin(θ)
where a and b are the lengths of two sides, and θ is the angle between them.
- a=EC=12cm
- b=CD=12cm
- θ=120∘
Substituting the values into the area formula:
Area=12×12×12×sin(120∘)
Using the sine value:
sin(120∘)=sin(180∘−60∘)=sin(60∘)=√32
Now substituting sin(120∘) back into the area formula:
Area=12×12×12×√32
=12×144×√32
=144√34
=36√3cm2
The area of triangle ECD is 36√3cm2.
Topper's Solved these Questions
Similar Questions
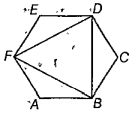
ABCDEF is a regular hexagon of side 12 cm. What is the area of traingle BDF?
View SolutionIn the given figure PQRSTU is a regular hexagon of side 12 cm. what is the area (in cm2) of triangle SQU?
दी गई आकृति में, PQRSTU एक समषट्भुज है जिसकी भुजा 12 से.मी. हे। त्रिभुज SQU का क्षेत्रफल (से.मी.2 में) क्या है?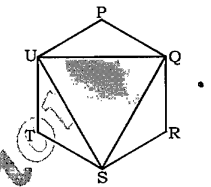
View Solution
Knowledge Check
ABCDEF is a regular hexagon of side 12 cm. What is the area (in cm2) of the triangle ECD?
A18√3B24√3C36√3D42√3ABCDEF is a regular hexagon of side 6 cm. What is the area of triangle BDF ?
 A32√3cm2B27√3cm2C24cm2Dnone of these
A32√3cm2B27√3cm2C24cm2Dnone of these
In the given figure, PQRS is a square of side 8 cm. ∠PQO=60∘. What is the area (in cm2) of the triangle POQ?
दी गई आकृति में, PQRS 8 से.मी. भुजा वाला एक वर्ग है। ∠PQO=60∘ है। त्रिभुज POQ का क्षेत्रफल (से.मी2 में) क्या है?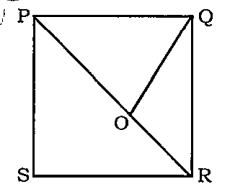
View SolutionABCDEF is a regular hexagon. What is the ratio of the area of triangle ACE and area of triangle AEF?
ABCDEF एक सम षटभुज है। त्रिभुज ACE के क्षेत्रफल तथा त्रिभुज AEF के क्षेत्रफल का अनुपात क्या है?
View SolutionThe perimeter of a right triangle is 60 cm and its hypotenuse is 26 cm. What is the area (in cm2) of the triangle ?
एक समकोण त्रिभुज की परिधि 60 cm है और इसका कर्ण 26 cm है। त्रिभुज का क्षेत्रफल (cm2 ) क्या है ?
View SolutionPQR is a right angled triangle in which PQ = QR. If the hypotenuse of the triangle is 20 cm, then what is the area (in cm2) of the triangle PQR?
PQR एक समकोण त्रिभुज है जिसमें PQ = QR है। यदि त्रिभुज का कर्ण 20 से.मी. हैं त्रिभुज PQR का क्षेत्रफल (से.मी.2 में) क्या हैं?
View SolutionIn the given figure, two squares of sides 8 cm and 20cm are given. What is the area (in cm2) of the shaded part?
दी गई आकृति में 8 से.मी. तथा 20 से.मी. भुजा वाले दो वर्ग दिये गये हैं छायांकित भाग का क्षेत्रफल (से.मी.2 में) क्या है?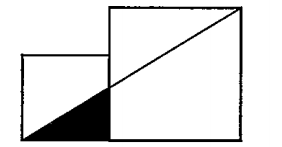
View SolutionIn the given figure, ABCDEF is a regular hexagon whose side is 12 cm. What is the shaded area (in cm2) ?
View Solution
