PQR is a right angled triangle in which PQ = QR. If the hypotenuse of the triangle is 20 cm, then what is the area (in cm2) of the triangle PQR?
PQR एक समकोण त्रिभुज है जिसमें PQ = QR है। यदि त्रिभुज का कर्ण 20 से.मी. हैं त्रिभुज PQR का क्षेत्रफल (से.मी.2 में) क्या हैं?
100√2
100
50√2
50
To find the area of triangle PQR, we follow these steps:
1. Identify the triangle type and dimensions:
- Triangle PQR is a right-angled triangle with PQ = QR. Let PQ = QR = x cm.
- The hypotenuse PR = 20 cm.
2. Apply the Pythagorean theorem:
- According to the Pythagorean theorem, in a right-angled triangle:
(hypotenuse)2=(side1)2+(side2)2
- Here, we have:
PR2=PQ2+QR2
- Substituting the known values:
202=x2+x2
- This simplifies to:
400=2x2
3. Solve for x:
- Rearranging the equation gives:
x2=4002=200
- Taking the square root of both sides:
x=√200=10√2 cm
4. Calculate the area of the triangle:
- The area A of a triangle is given by the formula:
A=12×base×height
- In this case, both the base and height are equal to x:
A=12×x×x=12×(10√2)×(10√2)
- Simplifying this gives:
A=12×100×2=100 cm2
5. Final answer:
- The area of triangle PQR is 100 cm2.
- Triangle PQR is a right-angled triangle with PQ = QR. Let PQ = QR = x cm.
- The hypotenuse PR = 20 cm.
- According to the Pythagorean theorem, in a right-angled triangle:
(hypotenuse)2=(side1)2+(side2)2
- Here, we have:
PR2=PQ2+QR2
- Substituting the known values:
202=x2+x2
- This simplifies to:
400=2x2
- Rearranging the equation gives:
x2=4002=200
- Taking the square root of both sides:
x=√200=10√2 cm
- The area A of a triangle is given by the formula:
A=12×base×height
- In this case, both the base and height are equal to x:
A=12×x×x=12×(10√2)×(10√2)
- Simplifying this gives:
A=12×100×2=100 cm2
- The area of triangle PQR is 100 cm2.
Topper's Solved these Questions
Similar Questions
The perimeter of a right triangle is 60 cm and its hypotenuse is 26 cm. What is the area (in cm2) of the triangle ?
एक समकोण त्रिभुज की परिधि 60 cm है और इसका कर्ण 26 cm है। त्रिभुज का क्षेत्रफल (cm2 ) क्या है ?
View SolutionIn the given figure PQRSTU is a regular hexagon of side 12 cm. what is the area (in cm2) of triangle SQU?
दी गई आकृति में, PQRSTU एक समषट्भुज है जिसकी भुजा 12 से.मी. हे। त्रिभुज SQU का क्षेत्रफल (से.मी.2 में) क्या है?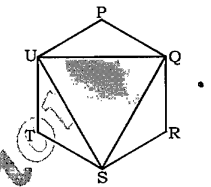
View Solution
Knowledge Check
PQR is a right angled triangle at Q in which PQ = QR. If the hypotenuse of the triangle is 20 cm, then what is the area (incm2) of the triangle PQR ?
A100√2B100C50√2D50In a triangle PQR, PX bisects QR. PX is the angle bisector of angle P. If PQ=12 cm and QX=3 cm, then what is the area (in cm2) of triangle PQR?
A12√3B8√15C18√2D9√15
In a right angled triangle PQR, PR is the hypotenuse of length 20 cm, ∠PRQ=30∘, the area of the triangle is
View SolutionIf the height of an equilateral triangle is 12 cm, then what is the area of the triangle?
यदि एक समबाह त्रिभुज की ऊंचाई 12 सेमी है, तो त्रिभुज का क्षेत्रफल कितना है?
View SolutionIn the given figure, PQRS is a square of side 8 cm. ∠PQO=60∘. What is the area (in cm2) of the triangle POQ?
दी गई आकृति में, PQRS 8 से.मी. भुजा वाला एक वर्ग है। ∠PQO=60∘ है। त्रिभुज POQ का क्षेत्रफल (से.मी2 में) क्या है?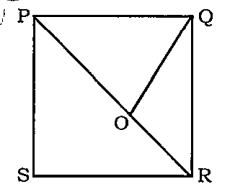
View SolutionIf sides of a triangle are 12cm, 15 cm and 21 cm, then what is the in-radius (in cm) of the triangle?
यदि एक त्रिभुज को भुजाएँ 12 सेमी., 15 सेमी. तथा 21 सेमी है, तो त्रिभुज की अंत त्रिज्या (सेमी. में) क्या है?
View SolutionTriangle PQR is inscribed in the circle whose radius is 14 cm. If PQ is the diameter of the circle and PR = 10cm, then what is thearea of the triangle PQR?
त्रिभुज PQR वृत्त जिसकी भुजा 14 से.मी. है, में अंकित है। यदि PQ वृत्त का व्यास है तथा PR = 10 सेमी. हैं, तो त्रिभुज PQR का क्षेत्रफल क्या हैं?
View SolutionPQRS is a parallelogram and its area is 300 cm2. Side PQ is extended to X such that PQ=QX. If XS intersects QR at Y, then what is the area (in cm2) of triangle SYR?
PQRS एक समांतर चतुर्भुज है तथा 300 से.मी.2 है। भुजा को तक इस तरह बढाया गया कि PQ=QX है। यदि XS, QR को Y पर काटता है, तो त्रिसुज SYR का क्षेत्रफल (से.मी.2 में) क्या हैं?
View Solution