A solid hemisphere has radius 14 cm. It is melted to form a cylinder such that the ratio of its curved
surface area and total surface area is 2:3. What is the radius (in cm) of its base?
एक ठोस अर्धगोले की तिज्या 14 से.मी. है। इसे पिघलाकर एक बेलन इस प्रकार बनाया जाता है कि उसके बक्र पृष्ठीय
क्षेत्रकल तथा कुल पृष्ठीय क्षेत्रफल का अनुपात 2 : 3 है। इसके आधार की त्रिज्या (से.मी. में) कया है?
103√3
143√3
73√3
213√3
To solve the problem step by step, we will follow these calculations:
Step 1: Understand the given data
We have a solid hemisphere with a radius of 14 cm. It is melted to form a cylinder, and we know the ratio of the curved surface area (CSA) to the total surface area (TSA) of the cylinder is 2:3.
Step 2: Write the formulas for the curved surface area and total surface area of the cylinder
- The formula for the curved surface area (CSA) of a cylinder is:
CSA=2πrh
- The formula for the total surface area (TSA) of a cylinder is:
TSA=2πr(r+h)
Step 3: Set up the equation based on the given ratio
According to the problem, we have:
CSATSA=23
Substituting the formulas:
2πrh2πr(r+h)=23
This simplifies to:
hr+h=23
Step 4: Cross-multiply to eliminate the fraction
Cross-multiplying gives:
3h=2(r+h)
Expanding this:
3h=2r+2h
Rearranging the terms:
3h−2h=2r
Thus, we find:
h=2r
Step 5: Calculate the volume of the hemisphere
The volume V of the hemisphere is given by:
V=23πR3
Substituting R=14 cm:
V=23π(14)3=23π×2744=54883π cm3
Step 6: Calculate the volume of the cylinder
The volume V of the cylinder is given by:
V=πr2h
Substituting h=2r:
V=πr2(2r)=2πr3
Step 7: Set the volumes equal
Since the volume of the melted hemisphere is equal to the volume of the cylinder:
54883π=2πr3
Dividing both sides by π:
54883=2r3
Multiplying both sides by 12:
54886=r3
Step 8: Calculate r3
Calculating 54886:
r3=914.6667
Step 9: Find r
Taking the cube root:
r=√(3)914.6667≈9.65 cm
Conclusion
Thus, the radius of the base of the cylinder is approximately 9.65 cm.
We have a solid hemisphere with a radius of 14 cm. It is melted to form a cylinder, and we know the ratio of the curved surface area (CSA) to the total surface area (TSA) of the cylinder is 2:3.
- The formula for the curved surface area (CSA) of a cylinder is:
CSA=2πrh
- The formula for the total surface area (TSA) of a cylinder is:
TSA=2πr(r+h)
According to the problem, we have:
CSATSA=23
Substituting the formulas:
2πrh2πr(r+h)=23
This simplifies to:
hr+h=23
Cross-multiplying gives:
3h=2(r+h)
Expanding this:
3h=2r+2h
Rearranging the terms:
3h−2h=2r
Thus, we find:
h=2r
The volume V of the hemisphere is given by:
V=23πR3
Substituting R=14 cm:
V=23π(14)3=23π×2744=54883π cm3
The volume V of the cylinder is given by:
V=πr2h
Substituting h=2r:
V=πr2(2r)=2πr3
Since the volume of the melted hemisphere is equal to the volume of the cylinder:
54883π=2πr3
Dividing both sides by π:
54883=2r3
Multiplying both sides by 12:
54886=r3
Calculating 54886:
r3=914.6667
Taking the cube root:
r=√(3)914.6667≈9.65 cm
Thus, the radius of the base of the cylinder is approximately 9.65 cm.
Topper's Solved these Questions
Similar Questions
A right circular solid cylinder has radius of base 7 cm and height is 28 cm. It is melted to form a cuboid such that the ratio of its side is 2: 3: 6. What is the total surface area (in cm2) cuboid?
एक सम वृत्ताकार ठोस बेलन के आधार की त्रिज्या 7 से.मी. तथा ऊँचाई 28 से.मी. है। इसे पिघलाकर एक घनाभ इस प्रकार बनाया जाता है कि उसकी भुजा का अनुपात 2:3:6 है। घनाभ का कूल पृष्ठिय क्षेत्रफल (से.मी.2 में) क्या हैं?
View SolutionA hemisphere is kept on top of a cube. Its front view is shown in the given figure the total height of the figure is 21cm. The ratio of curved surface area of hemisphere and total surface area of cube is 11 : 42. What is the total volume (in cm2) of figure?
एक अर्धगोला एक घन पर रखा गया है। इसके सामने का दृश्य आकृति में दर्शाया गया है। आकृति की कुल ऊँचाई 21 से.मी. हैं अर्धगोले के वक्र पृष्ठीय क्षेत्रफल तथा घन के कुल पृष्ठीय क्षेत्रफल का अनुपात 11 : 42 है। आकृति का कुल आयतन (से.मी.2 में) क्या है?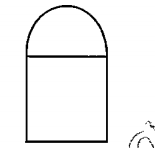
View Solution
Knowledge Check
What is the total surface area and the curved surface area of a solid hemisphere of radius 14cm ?
A924cm2,616cm2B5544cm2,1848cm2C1848cm2,1232cm2D2772cm2,1848cm2If the curved surface area of a cylinder is 1760cm2 and its base radius is 14 cm then its height is
A10 cmB15 cmC20 cmD40 cmA right circular solid cylinder has radius of base 7 cm and height is 28 cm. It is melted to form a cuboid such that the ratio of its side is 2 : 3 : 6. What is the total surface area (incm2) cuboid ?
A72x(1078)23B36x(2078)23C72x(2078)23D36x(1078)23
The ratio of the curved surface area and total surface area of a right circular cylitiderds 2 : 5. If the total surface area is 3080 cm2, then what is the volume (in cm3) of the cylinder?
एक लम्बवत वृत्ताकार बेलन के वक्र पृष्ठीय क्षेत्रफल तथा कुल पृष्ठोय क्षेत्रफल का अनुपात 2 : 5 है। यदि कूल पृष्ठीय क्षेत्रफल 3080 से.मी.2 है, तो बेलन का आयतन (से.मी.2 में) क्या है?
View SolutionA solid sphere has a radius 21 cm. It is melted to form a cube. 20% material is wasted in this process. The cube is melted to form hemisphere. In this process 20% material is wasted. The hemisphere is melted to form two spheres of equal radius. 20% material was also wasted in this process. What is the radius (in cm) of each new sphere?
एक ठोस गोले की त्रिज्या 21 से.मी. है। इसे पिघलाकर एक घन बनाया जाता है । इस प्रकिया में 20% सामग्री व्यर्थ हो जाती है। घन को पिघलाकर एक अर्धगोला बनाया जाता है। इस प्रकिया में 20% सामग्री व्यर्थ हो जाती है। अर्धगोला को पिघलाकर दो समान त्रिज्या वाले दो गोले बनाये जाते है। इस प्रकिया में भी 20% सामग्री व्यर्थ हो गई थी। प्रत्येक नए गोले की त्रिज्या (से.मी. में) क्या. है?
View SolutionThe total surface area of a solid cylinder is 1155cm2. Its curved surface area is equal to two-fifths of its total surface area. What is the height of the cylinder?
एक ठोस बेलन (सिलिंडर) का कुल पृष्ठ क्षेत्रफल 1155cm2 है | उसका वक्र पृष्ठ क्षेत्रफल, उसके कुल पृष्ठ क्षेत्रफल के2/5 के बराबर है | बेलन (सिलिंडर) की ऊंचाई (cm में) कितनी है? (π=227)
View SolutionIf the curved surface area of a solid cylinder is one-third of its total surface area, then what is the ratio of its diameter to its height ?
यदि किसी ठोस बेलन का वक्र पृष्ठ क्षेत्रफल इसके कुल पृष्ठ क्षेत्रफल का एक-तिहाई है, तो इसके व्यास और इसकी ऊंचाई में अनुपात ज्ञात करें |
View SolutionIf the curved surface area of a cylinder is 1320cm2 and its base radius is 21 cm, then its total surface area is :
View Solution
