The ratio of the curved surface area and total surface area of a right circular cylitiderds 2 : 5. If the total surface area is 3080 cm2, then what is the volume (in cm3) of the cylinder?
एक लम्बवत वृत्ताकार बेलन के वक्र पृष्ठीय क्षेत्रफल तथा कुल पृष्ठोय क्षेत्रफल का अनुपात 2 : 5 है। यदि कूल पृष्ठीय क्षेत्रफल 3080 से.मी.2 है, तो बेलन का आयतन (से.मी.2 में) क्या है?
4312√6
3822√6
4522√6
4642√6
To solve the problem step by step, we will follow the given information and derive the necessary values to find the volume of the cylinder.
Step 1: Understand the Ratios
We are given that the ratio of the curved surface area (CSA) to the total surface area (TSA) of a right circular cylinder is 2:5. This can be expressed mathematically as:
CSATSA=25
Step 2: Write the Formulas
The formulas for the curved surface area and total surface area of a cylinder are:
- Curved Surface Area (CSA) = 2πrh
- Total Surface Area (TSA) = 2πr(r+h)
Step 3: Set Up the Equation
From the ratio, we can write:
2πrh2πr(r+h)=25
This simplifies to:
hr+h=25
Step 4: Cross Multiply
Cross multiplying gives us:
5h=2(r+h)
Expanding this, we have:
5h=2r+2h
Rearranging gives:
3h=2r⇒rh=32
Let’s denote this as Equation (1).
Step 5: Use the Total Surface Area
We know the total surface area (TSA) is given as 3080 cm². Therefore:
2πr(r+h)=3080
Step 6: Substitute h in terms of r
From Equation (1), we can express h in terms of r:
h=23r
Substituting h into the TSA equation:
2πr(r+23r)=3080
This simplifies to:
2πr(53r)=3080
10πr23=3080
Step 7: Solve for r2
Multiplying both sides by 3:
10πr2=9240
Now, divide by 10π:
r2=924π
Step 8: Calculate r
Using π≈227:
r2=924×722=294
Thus,
r=√294=7√6 cm
Step 9: Find h
Using Equation (1):
h=23r=23(7√6)=14√63 cm
Step 10: Calculate the Volume
The volume V of the cylinder is given by:
V=πr2h
Substituting the values:
V=π(7√6)2(14√63)
Calculating r2:
(7√6)2=294
Thus,
V=π×294×14√63
V=294×14√6×π3
Calculating:
V=4116√63×227
V=4312√6 cm3
Final Answer
The volume of the cylinder is:
4312√6 cm3
We are given that the ratio of the curved surface area (CSA) to the total surface area (TSA) of a right circular cylinder is 2:5. This can be expressed mathematically as:
CSATSA=25
The formulas for the curved surface area and total surface area of a cylinder are:
- Curved Surface Area (CSA) = 2πrh
- Total Surface Area (TSA) = 2πr(r+h)
From the ratio, we can write:
2πrh2πr(r+h)=25
This simplifies to:
hr+h=25
Cross multiplying gives us:
5h=2(r+h)
Expanding this, we have:
5h=2r+2h
Rearranging gives:
3h=2r⇒rh=32
Let’s denote this as Equation (1).
We know the total surface area (TSA) is given as 3080 cm². Therefore:
2πr(r+h)=3080
From Equation (1), we can express h in terms of r:
h=23r
Substituting h into the TSA equation:
2πr(r+23r)=3080
This simplifies to:
2πr(53r)=3080
10πr23=3080
Multiplying both sides by 3:
10πr2=9240
Now, divide by 10π:
r2=924π
Using π≈227:
r2=924×722=294
Thus,
r=√294=7√6 cm
Using Equation (1):
h=23r=23(7√6)=14√63 cm
The volume V of the cylinder is given by:
V=πr2h
Substituting the values:
V=π(7√6)2(14√63)
Calculating r2:
(7√6)2=294
Thus,
V=π×294×14√63
V=294×14√6×π3
Calculating:
V=4116√63×227
V=4312√6 cm3
The volume of the cylinder is:
4312√6 cm3
Topper's Solved these Questions
Similar Questions
The ratio of the curved surface area to the total surface area of a right circular cylinder is 1:2. If the total surface area is 616 cm , what is the volume of the cylinder ?
View SolutionA hemisphere is kept on top of a cube. Its front view is shown in the given figure the total height of the figure is 21cm. The ratio of curved surface area of hemisphere and total surface area of cube is 11 : 42. What is the total volume (in cm2) of figure?
एक अर्धगोला एक घन पर रखा गया है। इसके सामने का दृश्य आकृति में दर्शाया गया है। आकृति की कुल ऊँचाई 21 से.मी. हैं अर्धगोले के वक्र पृष्ठीय क्षेत्रफल तथा घन के कुल पृष्ठीय क्षेत्रफल का अनुपात 11 : 42 है। आकृति का कुल आयतन (से.मी.2 में) क्या है?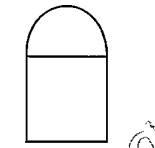
View SolutionA right circular cylinder is formed. A = sum of total surface area and the area of the two bases. B = the curved surface area of this cylinder. If A:B=3:2 and the volume of cylinder is 4312 cm3, then what is the sum of area (in cm2) of the two bases of this cylinder?
एक सम वृत्ताकार बेलन बनाया गया है । A=कुल पृष्ठिय क्षेत्रफल का योग तथा दो आधारों का क्षेत्रफल। B=इस बेलन का वक्र पृष्ठिय क्षेत्रफल। यदि A:B=3:2 तथा बेलन का आयतन 4312 से.मी.3 हैं, तो इस बेलन 1 तो बेलन के दोनो अधारो के क्षेत्रफल (से.मीः2 में) का योग है?
View SolutionThe radius of the base of a right circular cylinder is 3 cm and its curved surface area is 60πcm2 . The volume of the cylinder (incm3) is :
एक लम्ब वृत्तीय बेलन के आधार की त्रिज्या 3 सेमी है तथा इसका वक्र पृष्ठ क्षेत्रफल 60π वर्ग सेमी है | इस बेलन का आयतन होगा:
View SolutionIf the curved surface area of a solid cylinder is one-third of its total surface area, then what is the ratio of its diameter to its height ?
यदि किसी ठोस बेलन का वक्र पृष्ठ क्षेत्रफल इसके कुल पृष्ठ क्षेत्रफल का एक-तिहाई है, तो इसके व्यास और इसकी ऊंचाई में अनुपात ज्ञात करें |
View SolutionThe ratio of curved surface area and volume of a cylinder is 1: 7. The ratio of total surface area and volume is 187 : 770. What is the respective ratio of its base radius and height?
एक बेलन के वक्र पृष्ठीय क्षेत्रफल तथा आयतन का अनुपात 1 : 7 है। कूल पृष्ठोय क्षेत्रफल तथा आयतन का अनुपात 187 : 770 है। इसके आधार की त्रिज्या तथा ऊँचाई क्रमशः अनुपात क्या है? Option 1- 5 : 8 Option 2- 4 : 9 Option 3- 3 : 7 Option 4- 7 : 10
View SolutionA solid hemisphere has radius 14 cm. It is melted to form a cylinder such that the ratio of its curved surface area and total surface area is 2:3. What is the radius (in cm) of its base?
एक ठोस अर्धगोले की तिज्या 14 से.मी. है। इसे पिघलाकर एक बेलन इस प्रकार बनाया जाता है कि उसके बक्र पृष्ठीय क्षेत्रकल तथा कुल पृष्ठीय क्षेत्रफल का अनुपात 2 : 3 है। इसके आधार की त्रिज्या (से.मी. में) कया है?
View SolutionA prism has a regular hexagonal base with side 6cm. If the total surface area of prism is 216√3cm2, then what is the height (in cm) of prism?
एक प्रिज्म का आधार, एक 6 से.मी. भुजा वाला समषट्भुज हैं यदि प्रिज्म का कुल पृष्ठीय क्षेत्रफल 216√3से.मी.2 है तो प्रिज्म की लम्बाई (से.मी. में) क्या हे?
View SolutionIf the total surface area of a cube is 1944m2, then find the volume of the cube :
यदि एक घन का पृष्ठ क्षेत्रफल 1944m2 है , तो इसका आयतन है :
View SolutionThe total surface area of a solid cylinder is 1155cm2. Its curved surface area is equal to two-fifths of its total surface area. What is the height of the cylinder?
एक ठोस बेलन (सिलिंडर) का कुल पृष्ठ क्षेत्रफल 1155cm2 है | उसका वक्र पृष्ठ क्षेत्रफल, उसके कुल पृष्ठ क्षेत्रफल के2/5 के बराबर है | बेलन (सिलिंडर) की ऊंचाई (cm में) कितनी है? (π=227)
View Solution
