The area of a circle and a square are same. The ratio of the diagonal of the square to the radius of the circle is-
एक वृत्त और एक वर्ग का क्षेत्रफल एकसमान है। वर्ग की विकर्ण और वृत्त की त्रिज्या का अनुपात क्या होगा?
√π:1
1:π
√2√π:1
1:√π
To solve the problem, we need to find the ratio of the diagonal of a square to the radius of a circle, given that the areas of both shapes are equal.
1. Define Variables:
- Let the side length of the square be A.
- Let the radius of the circle be R.
2. Area of the Square:
- The area of the square is given by:
Area of square=A2
3. Area of the Circle:
- The area of the circle is given by:
Area of circle=πR2
4. Set the Areas Equal:
- According to the problem, the areas of the square and the circle are equal:
A2=πR2
5. Solve for A:
- Rearranging the equation gives:
A=√πR
6. Find the Diagonal of the Square:
- The diagonal D of the square can be calculated using the formula:
D=A√2
- Substituting A from the previous step:
D=√πR⋅√2=√2πR
7. Calculate the Ratio:
- We need to find the ratio of the diagonal of the square to the radius of the circle:
Ratio=DR=√2πRR=√2π
Final Answer:
The ratio of the diagonal of the square to the radius of the circle is:
√2π:1
- Let the side length of the square be A.
- Let the radius of the circle be R.
- The area of the square is given by:
Area of square=A2
- The area of the circle is given by:
Area of circle=πR2
- According to the problem, the areas of the square and the circle are equal:
A2=πR2
- Rearranging the equation gives:
A=√πR
- The diagonal D of the square can be calculated using the formula:
D=A√2
- Substituting A from the previous step:
D=√πR⋅√2=√2πR
- We need to find the ratio of the diagonal of the square to the radius of the circle:
Ratio=DR=√2πRR=√2π
The ratio of the diagonal of the square to the radius of the circle is:
√2π:1
Topper's Solved these Questions
Similar Questions
A square has been inscribed in a circle. What is the ratio of the length of side of the square to the radius of the circle?
एक वृत्त के अंदर एक वर्ग बनाया गया है| वर्ग की भुजा की लंबाई और वृत्त की त्रिज्या का अनुपात क्या है?
View SolutionA square has been inscribed in a circle. What is the ratio of the length of a side of the square to the radius of the circle ?
एक वर्ग किसी वृत्त के भीतर स्थित है | वर्ग की एक भुजा की लंबाई तथा वृत्त की त्रिज्या में अनुपात ज्ञात करें |
View Solution
Knowledge Check
The radius of a circle is a side of a square. The ratio of the areas of the circle and the square is
A2:πB1:πCπ:1Dπ:2The diameters of two circles are the side of a square and the diagonal of the square. The ratio of the areas of the smaller circle and the larger circle is
A1:2B1:4C√2:√3D1:√2
If the area of a square is decreased by 19%, then the diagonal of the square is decreased by :
यदि वर्ग का क्षेत्रफल 19% कम हो जाता है तो वर्ग का विकर्ण कितना कम हो जाता है|
View SolutionThe area of a square is 144cm2. What is the perimeter of the square formed by the diagonal of the original square as its side?
एक वर्ग का क्षेत्रफल 144 वर्ग सेमी है| आरंभिक वर्ग के विकर्ण को भुजा मानकर बनाए गए वर्ग का परिमाप क्या होगा ?
View SolutionThe area of a regular hexagon is equal to the area of the square. What is the ratio of the perimeter of the regular hexagon to the perimeter of square?
सम षटभुज का क्षेत्रफल वर्ग के क्षेत्रफल के बराबर है। सम षटभुज के परिमाप का वर्ग के परिमाप से क्या अनुपात है?
View SolutionThe diagonal of a square measures 6√2 cm. The measure of the diagonal of a square whose area is twice that of the first square is:
किसी वर्ग का विकर्ण 6√2 सेमी का है | उस वर्ग के विकर्ण का माप ज्ञात करें जिसका क्षेत्रफल पहले वर्ग के क्षेत्रफल से दोगुना है ?
View SolutionIn the given figure, the ratio of the area of the largest square to that of the smallest square is:
दी गयी आकृति में, सबसे बड़े वर्ग के क्षेत्रफल और सबसे छोटा वर्ग के क्षेत्रफल का अनुपात है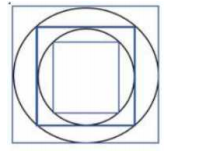
View SolutionThe area of square is 200m2. A new square is formed in such a way that the length of its diagonal is √2 times of the given square. Then the area of the new square formed is-
एक वर्ग का क्षेत्रफल 200 वर्ग मीटर है। एक नया वर्ग इस प्रकार बनाया गया है कि उसके विकर्ण की लंबाई पहले वर्ग के विकर्ण की √2 गुना के बराबर है, नये वर्ग का क्षेत्रफल है-
View Solution
