A is the centre of circle whose radius is 8 units and B is the centre of a circle whose diameter is 8 units. If these two circles touch externally, then
the area of the circle with radius AB is -
A,8 इकाई त्रिज्या वाले वृत्त का केन्द्र है और B, 8 इकाई व्यास वाले वृत्त का केन्द्र है ।यदि ये दोनों वृत्त बाहर से स्पर्श करते हैं, तो AB त्रिज्या वाले वृत्त का क्षेत्रफल कितना है ?
36 pi units^2//इकाई^2
64πunits2/इकाई2
144πunits2/इकाई2
256πunits2/इकाई2
To solve the problem, we need to find the area of the circle whose radius is equal to the distance between the centers of the two given circles, A and B.
1. Identify the Radius of Circle A:
- The radius of circle A is given as 8 units.
2. Identify the Radius of Circle B:
- The diameter of circle B is given as 8 units. Therefore, the radius of circle B is:
Radius of Circle B=Diameter2=82=4 units
3. Determine the Distance Between the Centers (AB):
- Since the two circles touch externally, the distance between their centers (AB) is the sum of their radii:
AB=Radius of Circle A+Radius of Circle B=8+4=12 units
4. Calculate the Area of the Circle with Radius AB:
- The area A of a circle is given by the formula:
A=πr2
- Here, r=AB=12 units. Thus, the area is:
A=π(12)2=π×144=144π square units
5. Final Answer:
- The area of the circle with radius AB is 144π square units.
- The radius of circle A is given as 8 units.
- The diameter of circle B is given as 8 units. Therefore, the radius of circle B is:
Radius of Circle B=Diameter2=82=4 units
- Since the two circles touch externally, the distance between their centers (AB) is the sum of their radii:
AB=Radius of Circle A+Radius of Circle B=8+4=12 units
- The area A of a circle is given by the formula:
A=πr2
- Here, r=AB=12 units. Thus, the area is:
A=π(12)2=π×144=144π square units
- The area of the circle with radius AB is 144π square units.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A is the centre of circle whose radius is 8 and B is the centre of a circle whose diameter is 8. If these two circles touch externally, then the area of the circle with diameter AB is
A36πB64πC144πD256πA chord of length 16 cm is drawn in a circle of radius 10 cm .Calculate the distance of the chord from the centre of the circle.
A8 cm / सेमी०B6 cm / सेमी०C4 cm / सेमी०D12 cm / सेमी०
What will be the area of a circle whose radius is √5 cm?
एक वृत्त का क्षेत्रफल क्या होगा जिसकी त्रिज्या √5 सेमी है ?
View SolutionWhat is the distance between two parallel tangents of a circle of radius 8 cm?
8 सेमी त्रिज्या वाले वृत्त की दो समानांतर स्पर्श रेखाओं के बीच की दूरी कितनी है?
View SolutionIf the length of a chord of a circle C at a distance of 12 cm from the centre is 10 cm, then the diaimeter of the circle is
यदि किसी वृत्त के केन्द्र से 12 सेमी. की दूरी पर जीवा की लंबाई 10 सेमी. है, तो वृत्त का व्यास है-
View SolutionPA and PB are tangents to the circle and O is the centre of the circle. The radius is 5 cm and PO is 13 cm. If the area of the triangle PAB is M, then the value of √M15 is :
PA और PB वृत्त के स्पर्शरेखा है और O वृत्त का केंद्र है। त्रिज्या 5 सेमी और PO =13 सेमी है। यदि त्रिभुज PAB का क्षेत्रफल M है, तो √M15 का मान है: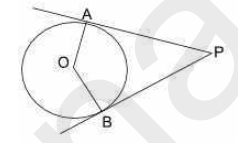
View SolutionIf the length of a side of a square is equal to the diameter of a circle, then the ratio between the areas of square and circle is (π=227)
यदि किसी वर्ग की भुजा की लम्बाई किसी वृत्त के व्यास के बराबर है, तब वर्ग तथा वृत्त के क्षेत्रफल का अनुपात हैः
View SolutionAB is a diameter of a circle with centre O. CB is a tangent to the circle at B. AC intersects the circle at G. If the radius of the circle is 6cm and AG = 8cm, then the length of BC is :
AB एक वृत्त का व्यास है जिसका केंद्र O है | CB, B पर वृत्त की स्पर्श रेखा है| AC, वृत्त को G पर काटता है | यदि वृत्त की त्रिज्या 6 सेमी है तथा AG = 8 सेमी है, तो BC की लंबाई ज्ञात करें |
View Solution
