In division sum, the divisor is 4 times the quotient and twice the remainder. If a and b are respectively the divisor and the divided, then
विभाजन के प्रश्न में, भाजक भागफल का 4 गुना और शेषफल का दोगुना हे। यदि a और b क्रमशः भाजक और भाज्य हैं, तो
4a−a2a=3
4b−2aa2=2
(a+1)2=4b
a(a+2)b=4
To solve the problem step by step, we will define the variables and use the relationships given in the question to find the relationship between the divisor (A) and the dividend (B).
1. Define Variables:
- Let A be the divisor.
- Let Q be the quotient.
- Let R be the remainder.
- Let B be the dividend.
2. Set Up Relationships:
- According to the problem, the divisor A is 4 times the quotient Q:
A=4Q
- The divisor A is also twice the remainder R:
A=2R
3. Express Quotient and Remainder in Terms of Divisor:
- From the first equation, we can express the quotient:
Q=A4
- From the second equation, we can express the remainder:
R=A2
4. Use the Division Formula:
- The relationship between the dividend, divisor, quotient, and remainder is given by:
B=(Q×A)+R
- Substitute Q and R into this formula:
B=(A4×A)+A2
5. Simplify the Expression:
- Calculate A4×A:
A24
- Now, substitute this back into the equation for B:
B=A24+A2
- To combine the terms, convert A2 to have a common denominator of 4:
A2=2A4
- Now, add the two fractions:
B=A24+2A4=A2+2A4
6. Final Relationship:
- Thus, we can express B in terms of A:
B=A(A+2)4
Conclusion:
The relationship between the divisor A and the dividend B is:
B=A(A+2)4
- Let A be the divisor.
- Let Q be the quotient.
- Let R be the remainder.
- Let B be the dividend.
- According to the problem, the divisor A is 4 times the quotient Q:
A=4Q
- The divisor A is also twice the remainder R:
A=2R
- From the first equation, we can express the quotient:
Q=A4
- From the second equation, we can express the remainder:
R=A2
- The relationship between the dividend, divisor, quotient, and remainder is given by:
B=(Q×A)+R
- Substitute Q and R into this formula:
B=(A4×A)+A2
- Calculate A4×A:
A24
- Now, substitute this back into the equation for B:
B=A24+A2
- To combine the terms, convert A2 to have a common denominator of 4:
A2=2A4
- Now, add the two fractions:
B=A24+2A4=A2+2A4
- Thus, we can express B in terms of A:
B=A(A+2)4
The relationship between the divisor A and the dividend B is:
B=A(A+2)4
Topper's Solved these Questions
Similar Questions
The divisor is 24 times the quotient and 8 times the remainder. If the quotient is 18, then the dividend is:
भाजक भागफल का 24 गुना और शेष 8 गुना है। यदि भागफल 18 है, तो लाभांश है:
View SolutionA divisor is 15 times the quotient and 3 times the remainder. If the remainder is 40, find the dividend.
एक भाजक, भागफल का 15 गुना तथा शेषफल का 3 गुना है। यदि शेषफल 40 है, तो भाज्य ज्ञात कीजिए।
View SolutionIn finding the HCF of two numbers by division method, the last divisor is 17 and the quotients are 1, 11 and 2, respectively. What is the sum of the two numbers ?
विभाजन विधि से दो संख्याओं का HCF निकालने के दौरान अंतिम भाजक 17 है तथा शेषफल क्रमशः 1, 11 तथा 2 हैं | दोनों संख्याओं का योग क्या है?
View SolutionThe ratio between the divisor and remainder is 3 : 2 and the ratio between the divisor and the quotient is 7 : 12. If remainder is 14, then find the remainder when the dividend is divided by 9.
भाजक तथा शेषफल का अनुपात 3:2 है और भाजक तथा भागफल का अनुपात 7:12 है | यदि शेषफल 14 है, तो भाज्य को 9 से विभाजित करने पर प्राप्त शेषफल है:
View SolutionWhen a number is successively divided by 3, 4 and 7, the remainder obtained are 2, 3 and 5 respectively. What will be the remainder when 84 divides the same number?
जब कोई संख्या क्रमिक रूप से 3, 4 और 7 से विभाजित होती है, तो प्राप्त शेष क्रमशः 2, 3 और 5 होते हैं। जब उसी संख्या को 84 से विभाजित करते हैं तो शेष क्या होगा ?
View SolutionIn the given triangle, D and E is the middle point of AF and AG, respectively, F and G are the midpoint of AB and AC respectively. If DE is 2.4 cm then what is the value of BC?
नीचे दिए गए त्रिभुज में , D और E क्रमश : AF और AG के मध्य बिंदु है , F और G क्रमश : AB और AC के मध्य बिंदु है | यदि DE =2.4 cm है तो BC का मान कया है?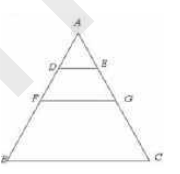
View SolutionWhen positive numbers x, y and z are divided by 31, the reminders are 17, 24 and 27 respectively. When (4x - 2y + 3z) is divided by 31, the reminder will be:
जब सकारात्मक संख्या x, y और z को 31 से विभाजित किया जाता है, तो शेषफल क्रमशः 17, 24 और 27 होते हैं। जब (4x - 2y + 3z) को 31 से विभाजित किया जाता है, तो शेषफल क्या होगा |
View SolutionLet x be the smallest number greater than 600 which gives the remainders 2, 3 and 4, when divided by 5, 6 and 7 respectively. The sum of digits of x is:
मान लीजिये कि x, 600 से बड़ी सबसे छोटी संख्या है जो 5, 6 और 7 से विभाजित होने पर शेषफल क्रमशः 2, 3 और 4 छोड़ती है | x के अंकों का जोड़ है -
View SolutionIn a quadrilateral ABCD, E is a point in the interior of the quadrilateral such that DE and CE are the bisector of ∠D and ∠C, respectively, If ∠B=82∘ and ∠DEC=80∘ then ∠A= ?
एक चतुर्भुज ABCD में, E, चतुर्भुज के भीतरी भाग का एक बिंदु इस प्रकार है की DE और CE क्रमश ∠D और ∠C, के द्विभाजक हैं, यदि ∠B=82∘और ∠DEC=80∘ तो ∠A = ?
View SolutionWhen positive number a, b and c are divided by 13, the remainder are 9, 7 and 10, respectively. What will be the remainder when (a + 2b + 5c) is divided by 13?
जब सकारात्मक संख्या A, B और C को 13 से विभाजित किया जाता है, तो शेष क्रमश 9, 7 और 10 होते हैं। जब (a + 2b + 5c) को 13 से विभाजित किया जाता है तो शेषफल कया होगा?
View Solution
