72% of the students of a certain class took Biology and 44% took Mathematics. If each student took at least one subject from Biology or Mathematics and 40 took both, then the total number of students in the class is
200
240
250
320
Step by step video & image solution for 72% of the students of a certain class took Biology and 44% took Mathematics. If each student took at least one subject from Biology or Mathematics and 40 took both, then the total number of students in the class is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
72% of the students of a certain class took Biology and 44% took Mathematics. If each student took at least one subject from Biology or Mathematics and 40 took both, then the total number of students in the class is
A200B240C250D320Out of the 60 students of class ,29 took Mathematics ,32 took Biology and 8 took none of the two subjects . How many students took both Mathermatics and Biology ?
A8B9C7D6In a class of 55 students, 40 like Science and 29 like Mathematics. If each student likes at least one subject, answer the following questions.
How many like only Science?A29B15C26D19
42% of the total number of student passed in a class test. How many students failed, if the total number of students in the class is 1450 ?
View SolutionStudy the following histogram of marks in mathematics (out of 50) of students in a class and answer the following questions.
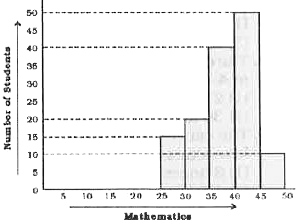
The total number of students in the class is :
View Solution90% of the students in a school passed in English, 85% passed in Mathematics and 150 students passed in both the subjects. If no student falled in both the sub jects, find the total number of stu dents.
View SolutionIn a class of 55 students. 40 like Science and 29 like Mathematics. If each student likes at least one subject, answer the following questions.
How many like both Science and Mathematics?
View SolutionIn a class of 35 students , 17 have taken Mathematics , 10 have taken mathematics but not economics if each student has taken either mathematics OR Economics or both , then the number of students who have taken Economics but not mathematics is
View Solution
