Prove that the tangent drawn at the mid point of an arc of a circle is parallel to the chord joining the end points of the arc.
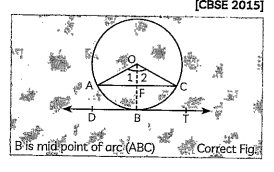
Step by step video & image solution for Prove that the tangent drawn at the mid point of an arc of a circle is parallel to the chord joining the end points of the arc. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The tangents drawn at the end points of the diameter of a circle will be
Aperpendicular to each otherBparallel to each otherCinclined to each other at 45∘Dinclined to each other at 60∘
Prove that the tangents drawn at the ends of the diameter of a circle are parallel.
View SolutionProve that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
View SolutionShow that tangent lines at the end points of a diameter of a circle are parallel.
View SolutionProve that the line joining the mid-points of two parallel chords of a circle passes through the centre.
View SolutionProve that the lengths of tangents drawn from an external point to a circle are equal.
View SolutionAn arc of a circle is called a_____if the ends of the arc on the ends of a diameter.
View SolutionProve that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
View Solution

