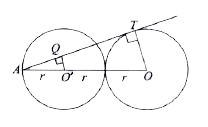
In fig 7, two equals circles, with centres O and O', touch each other at X. OO' produced meets the circle with centre O' at A. Ac is tangent to the circle with centre O, at the point C. O'D is perpendicular to AC. Find the value of (DO')/(CO).
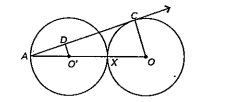
Step by step video & image solution for In fig 7, two equals circles, with centres O and O', touch each other at X. OO' produced meets the circle with centre O' at A. Ac is tangent to the circle with centre O, at the point C. O'D is perpendicular to AC. Find the value of (DO')/(CO). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
. In the given figure, two equal circles, with centres O and O', touch each other at X. OO' produced me the circle with centre O' at A. AC is tangent to the circle with centreO, at the point C. O'D is perpendicular to AC. Find the value of DO'CO.
View SolutionAC is tangent to O, O'D is ⊥ to AC, Find the value of DO'CO
View Solution
Knowledge Check
- Question 1 - Select One
AB and AC are tangents to the circle with centre O. Then x equals.
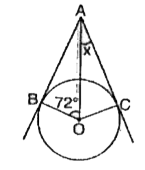 A22∘B18∘C20∘D36∘
A22∘B18∘C20∘D36∘ - Question 2 - Select One
In the given figure, AC is the diameter of the circle with centre O. Chord BD is perpendicular to AC. Express p in terms of x.
 Ax/2B90∘+x/2C90∘−x/2D180∘−x
Ax/2B90∘+x/2C90∘−x/2D180∘−x - Question 3 - Select One
TP and TQ are the tangents to a circle, with centre O. Find x.
 A15∘B60∘C30∘D45∘
A15∘B60∘C30∘D45∘
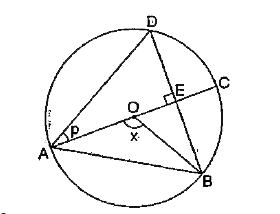
In the figure, two circles with centers O and P intersect each other at points D and C. Line AB intersects the circle with centre O at points A and B and touches the circle with centre P at point E. Prove ∠ADE+∠BCE=180∘.
 View Solution
View SolutionIf Fig , AOB is diameter of a circle with centre O and AC is a tangent to the circle at A . If ∠BOC=130∘ , then find ∠ACO .
 View Solution
View SolutionIf O is the centre of the circle, then x is
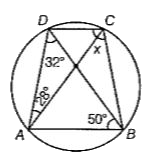 View Solution
View SolutionIf O is the centre of the circle, then x is
 View Solution
View SolutionTwo circles of same radius r centred at O and O' touch each other at P as shown in the figure, if OO' is produced to meet the circle C(O'r) at A and AT is a tangent to the circle C(O,r) such that O'Q ⊥ AT . Then AO : AO'=
 View Solution
View Solution

