The ratio of areas of two similar triangles is equal to the ratio of the squares of corresponding…….Solution in Telugu
Step by step video & image solution for The ratio of areas of two similar triangles is equal to the ratio of the squares of corresponding……. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In △ABC, DE∣∣BC and AD=13BD.
If BC = 4.5cm, Find DE.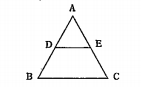
View SolutionWhich of the following are sets? Justify your answer.
The collection of all even integers.
View SolutionThe median of the data x/5, x, x/4, x/2 and x/8 is 8. Find the value of x.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
View SolutionThe ratio of area of Two similar triangles is equal to the ratio of the squares of any two corresponding sides.
View SolutionThe ratio of the the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides/altitudes.
View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
View SolutionThe ratio of areas of two similar triangles is equal to the ratio of the squares of corresponding…….
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that " the ratio of areas of two similar triangles is equal to the square of the ratio of their altitudes.
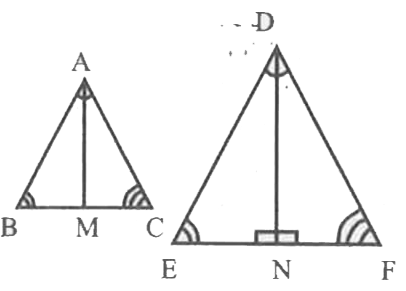
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio at the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View Solution
