The median and mean of a distribution of 29 and 32 respectively then modeSolution in Telugu
25.5
23
18
30.5
Step by step video & image solution for The median and mean of a distribution of 29 and 32 respectively then mode by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - BEYOND PUBLICATIONCHAPTER - STATISTICSEXERCISE - EXERCISE141videos
STATISTICS
- BOOK - BEYOND PUBLICATIONCHAPTER - SIMILAR TRIANGLESEXERCISE - EXERCISE143videos
SIMILAR TRIANGLES
- BOOK - BEYOND PUBLICATIONCHAPTER - TANGENTS AND SECANTS TO CIRCLEEXERCISE - EXERCISE157videos
TANGENTS AND SECANTS TO CIRCLE
Similar Questions
The median of the data x/5, x, x/4, x/2 and x/8 is 8. Find the value of x.
02:57View SolutionIn △ABC, DE∣∣BC and AD=13BD.
If BC = 4.5cm, Find DE.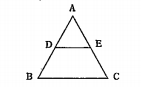
02:04View SolutionA tangent to a circle intersects it in ………. Point (s) .
02:13View SolutionIf the sum of the mode and mean of a certain frequency distribution is 129 and the median of the observations is 63, mode and median are respectively
01:56View SolutionThe median and mode of a frequency distribution are 26 and 29 respectively. Then , the mean is
01:05View Solutionएक बारम्बारता बंटन की माध्यिका तथा बहुलक क्रमश: 26 तथा 29 है तब माध्य ज्ञात कीजिये ।
View SolutionIf the mode and median of a frequency distribution are 31 and 37 respectively, find the arithmetic mean.
01:06View SolutionIf the mean and median of a frequency distribution are 35 and 33 respectively, find mode.
01:12View SolutionThe mean and the median of a distribution are 45.9 and 46 respectively. The mode will be
01:01View SolutionIf in a frequency distribution, the mean and median are 21 and 22 respectively, then its mode is approximately :
02:08View SolutionIn a frequency distribution , the mean and median are 21 and 22 respectively , then its mode is approximately
00:57View SolutionIf in a frequency distribution, the mean and median are 21 and 22 respectively, then its mode is approximately
01:56View SolutionThe median and mode of a frequency distribution are 26 and 29 then its mean is
View SolutionIf the median and mean of moderately asymmetrical frequency distribution are 72 and 74 respectively, then the mode is
01:42View SolutionFor a frequency distribution, Mode-Median = . . . . . × (Median-Mean)
02:46View Solution