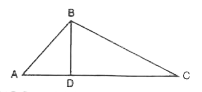
Answer any One queation : Prove that, if a perpendicular is draw on the hypotenuse from the right angled triangle, two triangles so formed on the two sides of the perpendicular are each similar to the original triangle and also similar to each other.Solution in Bengali
Step by step video solution for Answer any One queation : Prove that, if a perpendicular is draw on the hypotenuse from the right angled triangle, two triangles so formed on the two sides of the perpendicular are each similar to the original triangle and also similar to each other. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The population of the village increases by r% each year. If P be the population aftern years, then population n years ago was
View SolutionMultiple Choice Questions (MCQ) If r, 8, 16, q are in continued proportion, then the value of (p + q) is
View SolutionIf a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.
View Solutionएक समकोण त्रिभुज की एक भुजा पर समान कोण वाला त्रिभुज खींचा गया है | जिसमे लम्ब, आधार का दोगुना है | तो सिद्ध कीजिए कि कर्ण पर त्रिभुज का क्षेत्रफल वही है जो अन्य दो त्रिभुजों के क्षेत्रफलो का योग है |
View SolutionTheorem 6.7 : If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
View Solutionसिद्ध कीजिए की दो समकोण त्रिभुजों में यदि एक त्रिभुज का कर्ण व एक भुजा दूसरे त्रिभुज के कर्ण व संगत भुजा के अलग-अलग बराबर हो, तो वे त्रिभुज सर्वांगसम होते है।
View Solutionఒక లంబకోణ త్రిభుజాములో, లంబకోణము కలిగిన శీర్షము నుండి కర్ణనికి లంబము గీసిన, ఆ లాంబానికి ఇరువైపులా ఏర్పడిన త్రిభుజాలు, ఇచ్చిన త్రిభుజనికి సరూపాలు మరియు అవి ఒకదానికొకటి కూడా సరూపాలు.
View SolutionTheorem 6.7 : If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
View SolutionIf a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.
View SolutionIf a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.
View SolutionΔABC में, ∠B समकोण हैं। भुजा AC पर BD लम्ब हैं, तो सिद्ध कीजिए कि ΔABC के समरूप ΔBDC है।
View Solutionयदि एक समकोण त्रिभुज की दो भुजाएँ, दूसरे समकोण त्रिभुज की एक भुजा तथा कर्ण के बराबर है तब दो समकोण त्रिभुज सर्वांगसम है।
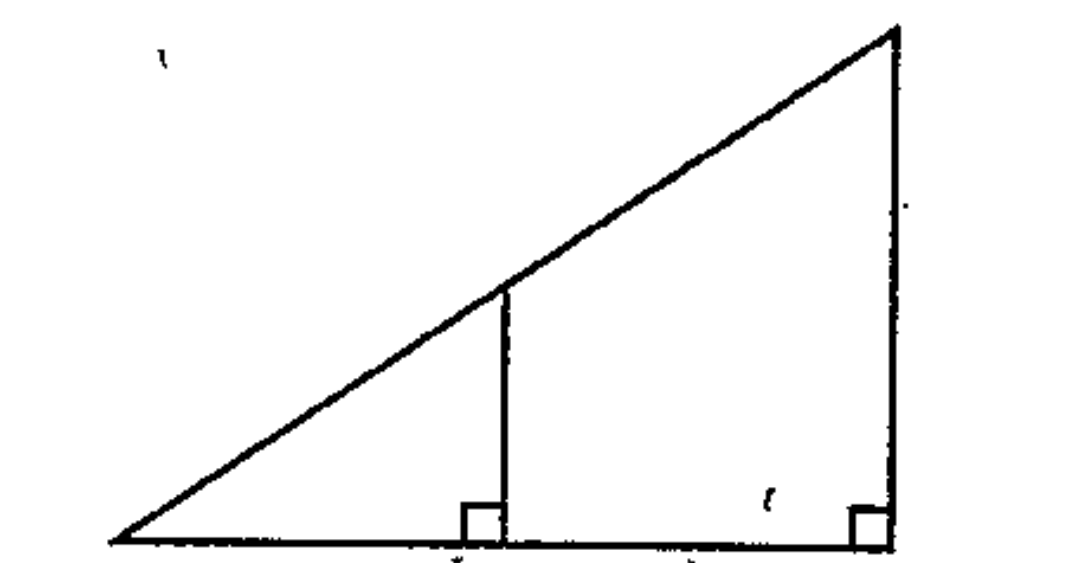
View SolutionDraw a right triangle and the perpendicular from the midpoint of the of the hypotenuse to the base
Prove that this perpendicular is half the perpendicular side of the large triangle.
 .
.
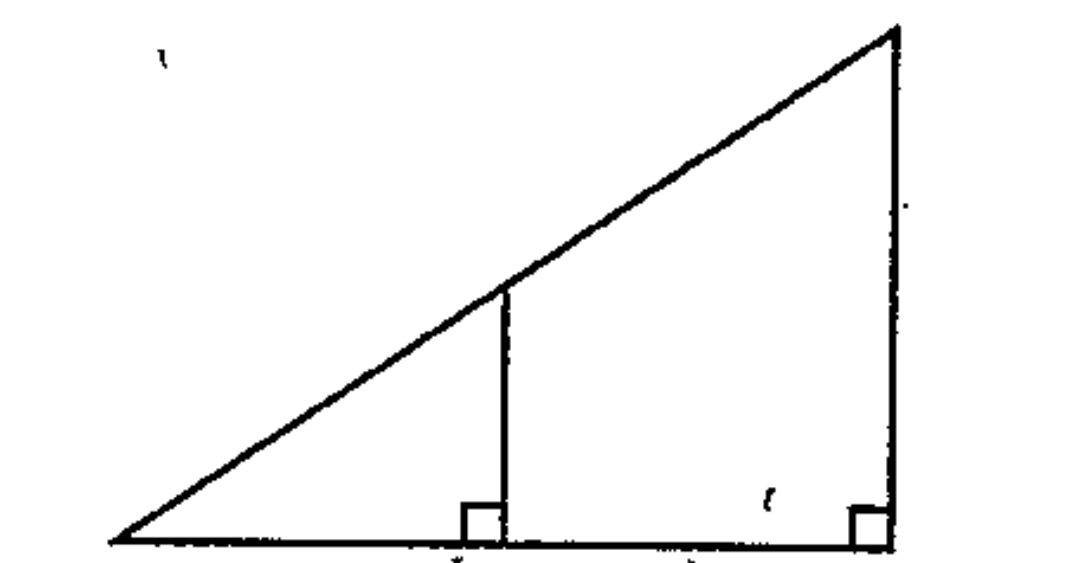
View SolutionDraw a right triangle and the perpendicular from the midpoint of the of the hypotenuse to the base
Prove that perpendicular bisects the bottom side of the larger triangle.
 .
.
View SolutionDraw a right triangle and the perpendicular from the midpoint of the of the hypotenuse to the base
Prove that the circumcentre of a right triangle is the midpoint of its hypotenuse.
 .
.
View Solutionthe two triangles formed by drawing perpendicular from right angle to the hypotenuse of a right angled triangle are similar and both of them are similar to the original triangle.
View Solution
