Two vertices of a rectangle are on the positive x-axis. The other two vertices lie on the lines y=4xandy=−5x+6. Then the maximum area of the rectangle is: 43 (b) 35 (c) 45 (d) 34
Step by step video & image solution for Two vertices of a rectangle are on the positive x-axis. The other two vertices lie on the lines y=4xa n dy=-5x+6. Then the maximum area of the rectangle is: 4/3 (b) 3/5 (c) 4/5 (d) 3/4 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
View SolutionA rectangle has two opposite vertices at the points (1, 2) and (5,5). It these vertices lie on the line x=3 , find the other vertices of the rectangle.
View SolutionThe points (1,3) and (5,1) are two opposite vertices of a rectangle. The other two vertices lie on the line the y=2x+c. Find c
View SolutionThe equation of one side of a rectangle is 3x−4y−10=0 and the coordinates of two of its vertices are (−2,1)and(2,4). Then, the area of the rectangle is
View SolutionA rectangle ABCD is inscribed in a circle with a diameter lying along the line 3y=x+10. If A=(-6,7), B=(4,7) then the area of the rectangle is
View SolutionA rectangle has two opposite vertices at the points (1,2) and (5,5). If the other vertices lie on the line x=3 , find the equations of the sides of the rectangle.
View SolutionFind the area bounded by the lines y=4x+5,y=5−xand4y=x+5.
View SolutionThe two opposite vertices of a square are (1,-6)and (5,4). Find the coordinates of the other two vertices.
View SolutionFour particles, each with mass m are arranged symmetrically about the origin on the x axis. A fifth particle, with mass M, is on the y axis. The direction of the gravitational force on M is:
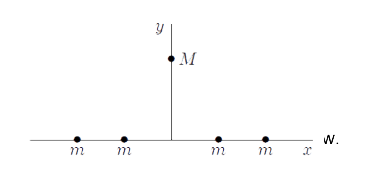
View Solutiony2+4(x−a2)=0. One of the vertexes of Δ'(Δ) is a vertex of the given parabola and other two vertices are the points where parabola meets their axis. If area of triangle is 250.Then a will be (A) 5 (B) 5√3 (C) 25√3 (D)3√5
View Solution
