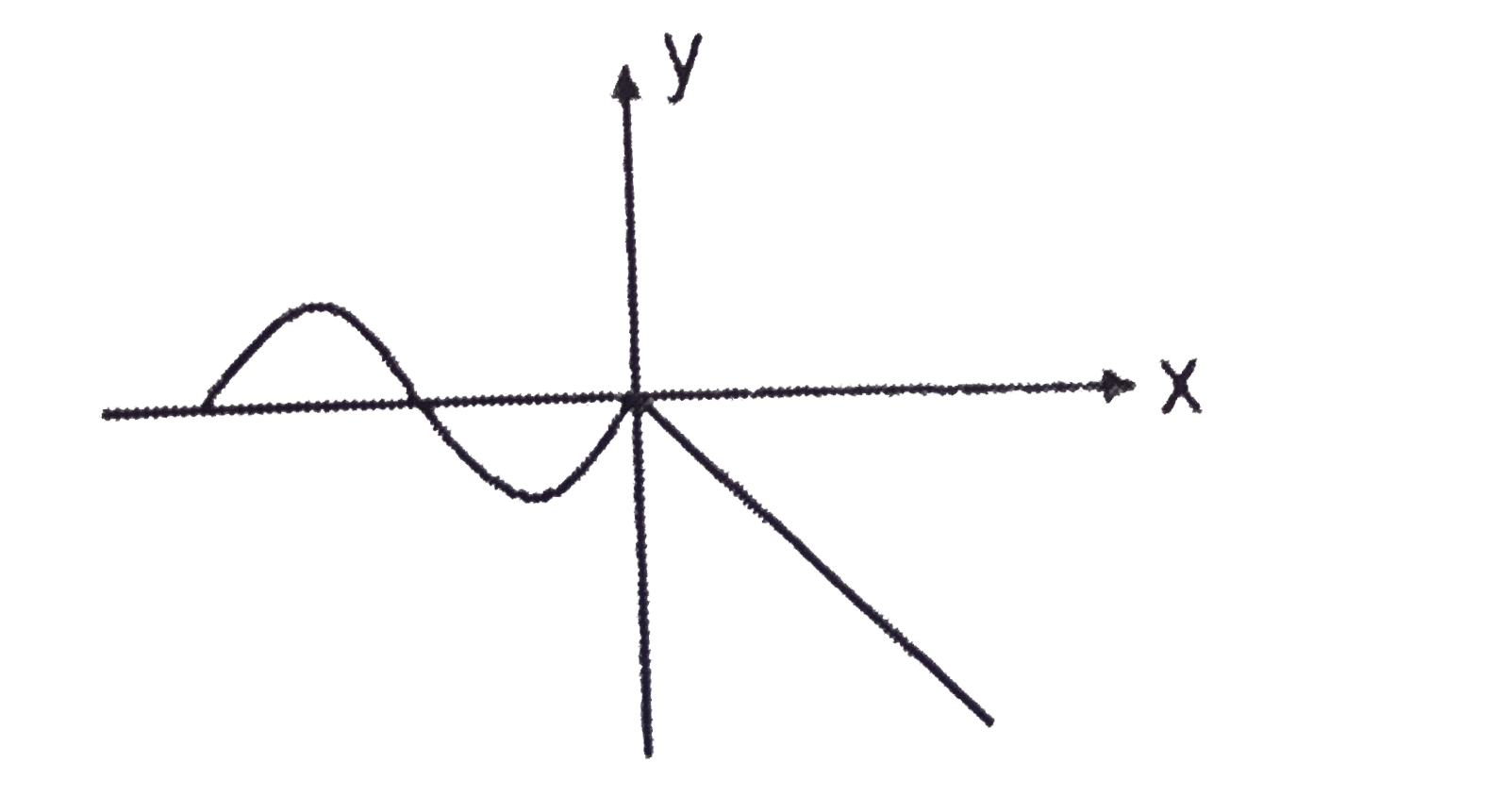
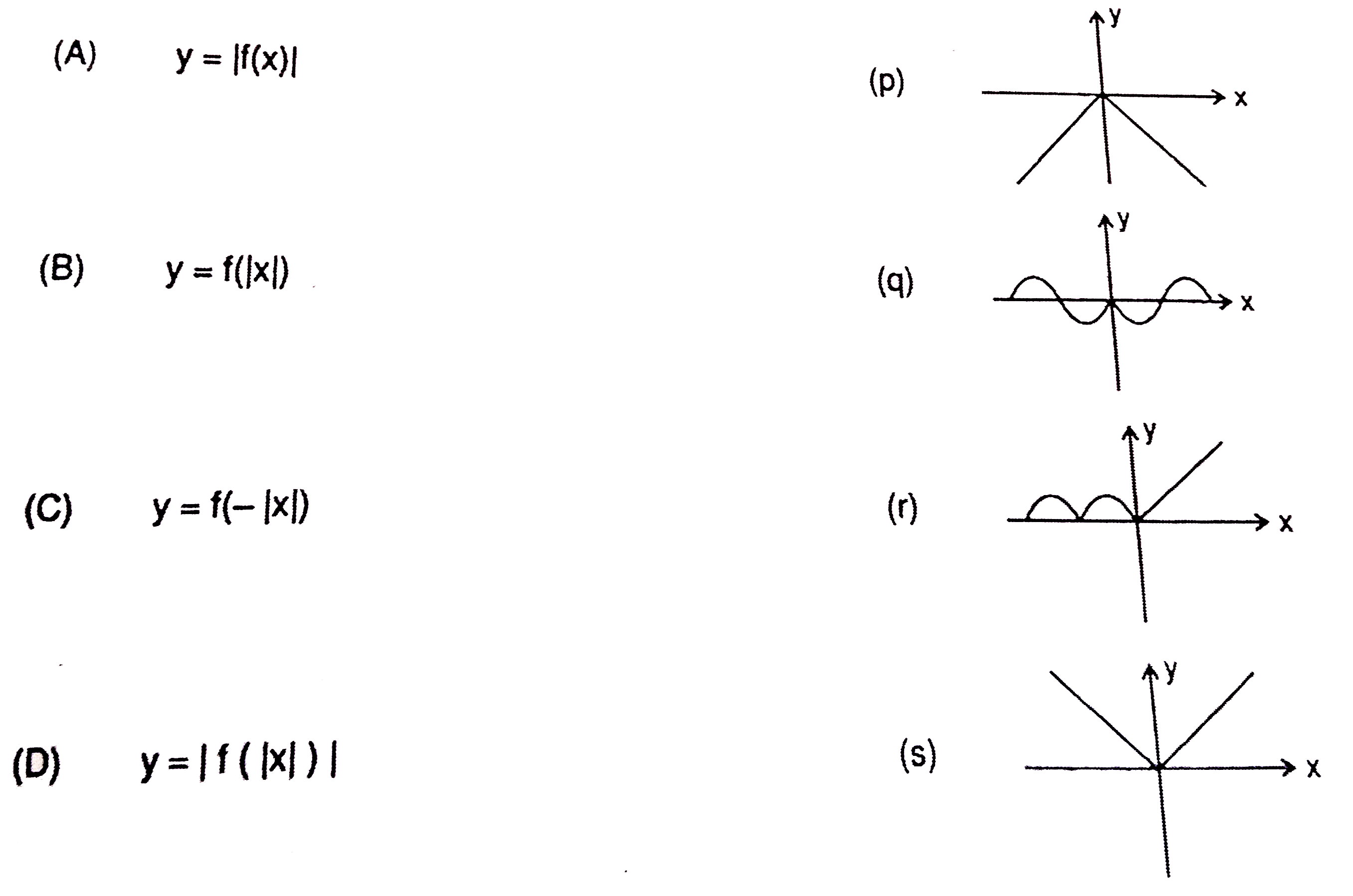If y=f(x) has following graph, then match the column.
To solve the problem of matching the functions with their corresponding graphs based on the given transformations, we will analyze each function step by step.
Step 1: Analyze the function y=|f(x)|
1. Understanding the Transformation: The function y=|f(x)| reflects any part of the graph of f(x) that is below the x-axis to above the x-axis.
2. Graph Construction:
- Retain the portions of the graph of f(x) that are above the x-axis.
- Reflect the portions of the graph that are below the x-axis to the positive y-axis.
3. Result: This results in a graph that is the same as f(x) for y≥0 and the mirror image for y<0.
Match: This matches with option R.
Step 2: Analyze the function y=f(|x|)
1. Understanding the Transformation: The function y=f(|x|) means that for negative values of x, the function will take the same values as those for positive x.
2. Graph Construction:
- For x≥0, the graph remains the same as f(x).
- For x<0, the graph mirrors the positive side of the graph.
3. Result: This results in a symmetric graph about the y-axis.
Match: This matches with option P.
Step 3: Analyze the function y=f(−|x|)
1. Understanding the Transformation: The function y=f(−|x|) reflects the graph of f(x) across the y-axis and then takes the negative of these values.
2. Graph Construction:
- For x≥0, we take f(−x).
- For x<0, we take f(−(−x))=f(x) and then negate it.
3. Result: This results in a graph that is entirely in the negative y-axis.
Match: This matches with option Q.
Step 4: Analyze the function y=|f(|x|)|
1. Understanding the Transformation: The function y=|f(|x|)| combines the effects of both absolute values.
2. Graph Construction:
- First, apply f(|x|) to get a symmetric graph.
- Then apply the absolute value to ensure all y-values are non-negative.
3. Result: This results in a graph that is entirely above the x-axis.
Match: This matches with option S.
Final Matches:
- A matches with R
- B matches with P
- C matches with Q
- D matches with S
Summary of Matches:
- A → R
- B → P
- C → Q
- D → S
2. Graph Construction:
- Retain the portions of the graph of f(x) that are above the x-axis.
- Reflect the portions of the graph that are below the x-axis to the positive y-axis.
3. Result: This results in a graph that is the same as f(x) for y≥0 and the mirror image for y<0.
2. Graph Construction:
- For x≥0, the graph remains the same as f(x).
- For x<0, the graph mirrors the positive side of the graph.
3. Result: This results in a symmetric graph about the y-axis.
2. Graph Construction:
- For x≥0, we take f(−x).
- For x<0, we take f(−(−x))=f(x) and then negate it.
3. Result: This results in a graph that is entirely in the negative y-axis.
2. Graph Construction:
- First, apply f(|x|) to get a symmetric graph.
- Then apply the absolute value to ensure all y-values are non-negative.
3. Result: This results in a graph that is entirely above the x-axis.
- A matches with R
- B matches with P
- C matches with Q
- D matches with S
- A → R
- B → P
- C → Q
- D → S
Topper's Solved these Questions
Similar Questions
Knowledge Check
The quadratic y=f(x) is shown above. Which of the following graphs represents the function y=f(x+3)−4?A B
B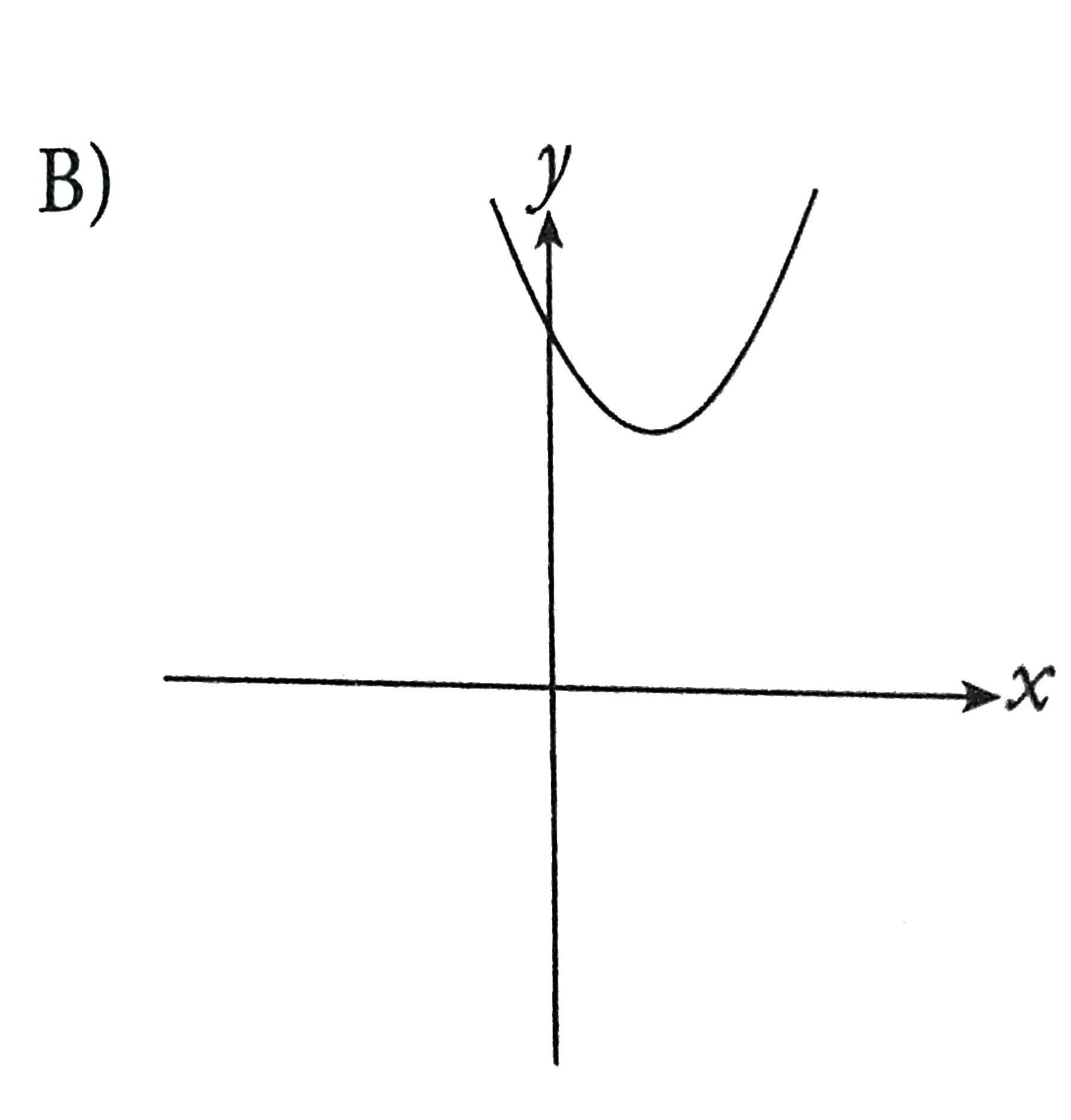 C
C D
D
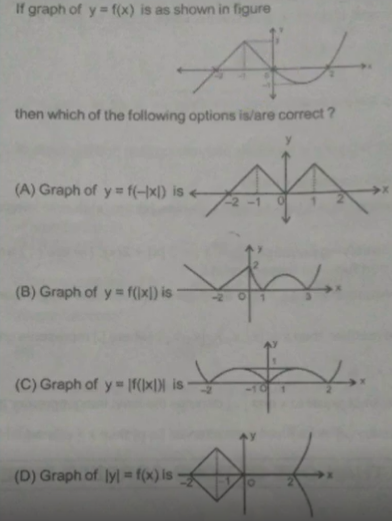
If graph of y= f(x) is as shown in figure, then which of the following options is/are correct?
View SolutionMatch the following columns I with column II.

View SolutionMatch the following columns.

View SolutionMatch the following columns.
View SolutionMatch the following columns.

View SolutionMatch the following columns.

View SolutionMatch the following column
View Solution