The statement (a+ib)<(c+id) is true for a2+b2=0 (b) b2+d2=0 b2+c2=0 (d) None of these
To solve the problem, we need to analyze the statement (a+ib)<(c+id) and determine under what conditions this inequality can hold true.
1. Understanding the Comparison of Complex Numbers:
- Complex numbers cannot be directly compared using the less than (<) or greater than (>) operators. The comparison can only be made based on their real parts or their moduli.
2. Separating Real and Imaginary Parts:
- The complex number can be expressed as:
- \( z_1 = a + ib \)
- \( z_2 = c + id \)
- For the inequality \( z_1 < z_2 \) to hold, we need to focus on the real parts since the imaginary parts will affect the comparison.
3. Setting Imaginary Parts to Zero:
- To make the comparison valid, we can set the imaginary parts \( b \) and \( d \) to zero:
- \( b = 0 \)
- \( d = 0 \)
- This simplifies our comparison to \( a < c \).
4. Identifying Conditions for Validity:
- Since we set \( b = 0 \) and \( d = 0 \), we can see that:
- \( b^2 + d^2 = 0 \)
- This condition is satisfied when both \( b \) and \( d \) are zero.
5. Checking Other Options:
- We check the other options:
- \( a^2 + b^2 = 0 \): This implies both \( a \) and \( b \) must be zero, which does not help in comparing \( a \) and \( c \).
- \( b^2 + c^2 = 0 \): This implies both \( b \) and \( c \) must be zero, which again does not help in the comparison.
- Therefore, the only valid condition is \( b^2 + d^2 = 0 \).
Conclusion:
The statement (a+ib)<(c+id) is true for the condition \( b^2 + d^2 = 0 \).
Final Answer:
(b) \( b^2 + d^2 = 0 \)
---
- Complex numbers cannot be directly compared using the less than (<) or greater than (>) operators. The comparison can only be made based on their real parts or their moduli.
- The complex number can be expressed as:
- \( z_1 = a + ib \)
- \( z_2 = c + id \)
- For the inequality \( z_1 < z_2 \) to hold, we need to focus on the real parts since the imaginary parts will affect the comparison.
- To make the comparison valid, we can set the imaginary parts \( b \) and \( d \) to zero:
- \( b = 0 \)
- \( d = 0 \)
- This simplifies our comparison to \( a < c \).
- Since we set \( b = 0 \) and \( d = 0 \), we can see that:
- \( b^2 + d^2 = 0 \)
- This condition is satisfied when both \( b \) and \( d \) are zero.
- We check the other options:
- \( a^2 + b^2 = 0 \): This implies both \( a \) and \( b \) must be zero, which does not help in comparing \( a \) and \( c \).
- \( b^2 + c^2 = 0 \): This implies both \( b \) and \( c \) must be zero, which again does not help in the comparison.
- Therefore, the only valid condition is \( b^2 + d^2 = 0 \).
The statement (a+ib)<(c+id) is true for the condition \( b^2 + d^2 = 0 \).
(b) \( b^2 + d^2 = 0 \)
Topper's Solved these Questions
Similar Questions
Statement - I : The statement that circumradius and inradius of a triangle are 12 and 8 respectively can not be correct.. Because : Statement - II : Circumradius ≥2 (inradius) A (b) B (c) C (d) D
View SolutionLet A and B be two 2×2 matrices. Consider the statements (i) AB=0⇒A=0orB=0 (ii)AB=I2⇒A=B−1 (a) only (i) (b) only (ii) (c) both are correct (d) none of these.
View Solution
Knowledge Check
Compare the statements A with B.
Statement A: Ranikhet disease is the disease of poultry
Statement B: It is caused by a virus.ABoth the statements A and B are correct.BStatement A is correct and B is wrongCStatement A is wrong and B is correctDNone of the above
Let AandB be two 2×2 matrices. Consider the statements (i) AB=O⇒A=OorB=O (ii)AB=I2⇒A=B−1 (iii) (A+B)2=A2+2AB+B2 (a)(i) and (ii) are false, (iii) is true (b)(ii) and (iii) are false, (i) is true (c)(i) is false (ii) and, (iii) are true (d)(i) and (iii) are false, (ii) is true
View SolutionStatement 1 : The statement A→(A→B). Is equivalent to A→(A∨B)
statement 2 : The statement ~[(A∧B)→(~A∨B)] is a tautology
View SolutionMatch the statements (A, B, C, D) in Column I with the statements (p, q, r, s) in column II. The answers are to be properly bubbled.
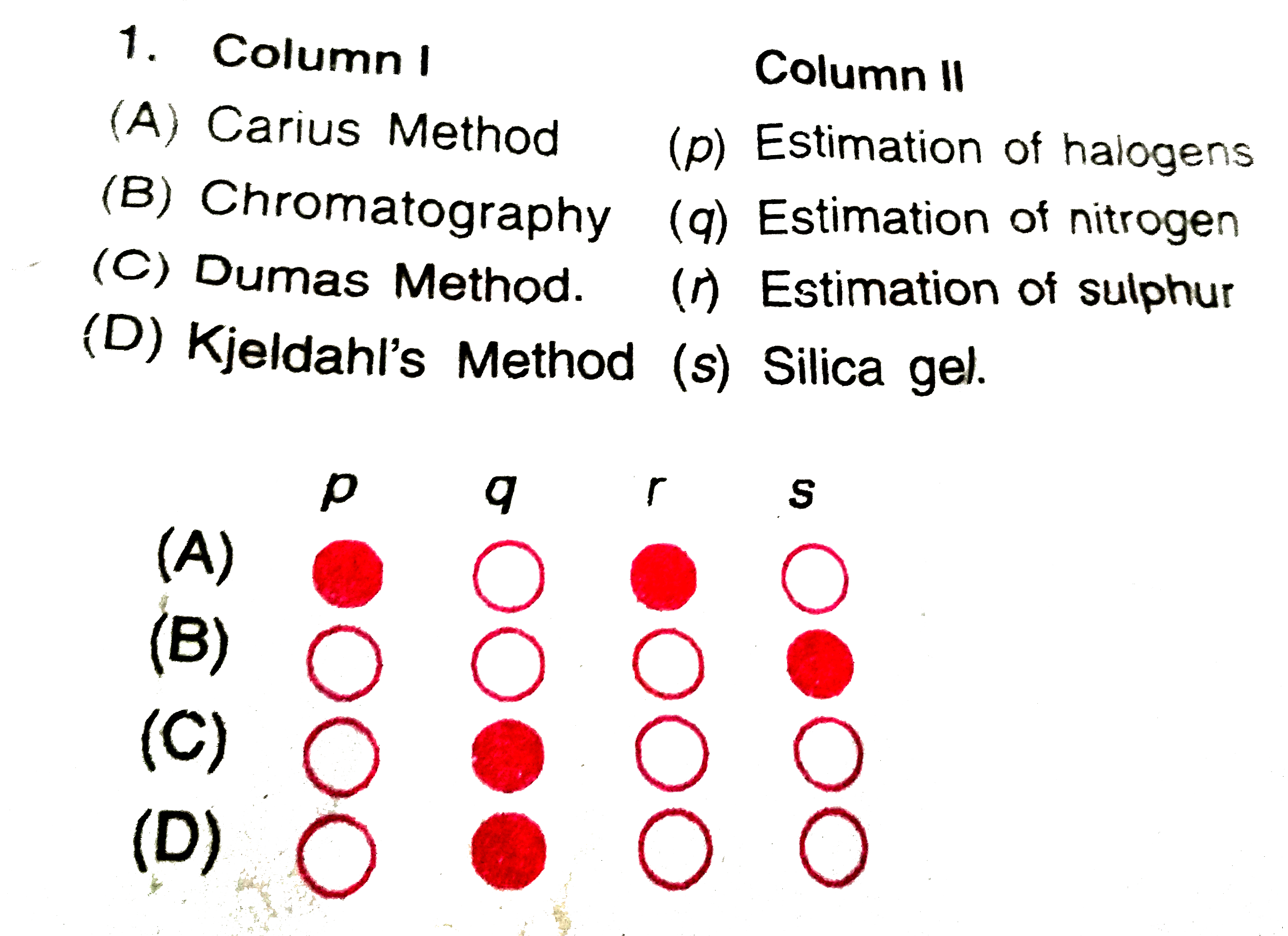
View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View Solution
