Let AandB be two 2×2 matrices. Consider the statements (i) AB=O⇒A=OorB=O (ii)AB=I2⇒A=B−1 (iii) (A+B)2=A2+2AB+B2 (a)(i) and (ii) are false, (iii) is true (b)(ii) and (iii) are false, (i) is true (c)(i) is false (ii) and, (iii) are true (d)(i) and (iii) are false, (ii) is true
(i) and (ii) are false, (iii) is true
(ii) and (iii) are false, (i) is true
(i) is false, (ii) and (iii) are true
(i) and (iii) are false, (ii) is true
The correct Answer is:D
To solve the problem, we need to analyze each statement regarding the matrices A and B and determine their validity. Let's go through each statement step by step.
Step 1: Analyze Statement (i)
Statement: AB=O⇒A=O or B=O
Analysis:
This statement claims that if the product of two matrices A and B is the zero matrix O, then at least one of the matrices must be the zero matrix.
Counterexample:
Let:
A=(1000),B=(0001)
Calculating AB:
AB=(1000)(0001)=(0100)≠O
Now let’s take:
A=(1000),B=(0000)
Calculating AB:
AB=(1000)(0000)=(0000)=O
In this case, A≠O and B=O. However, we can also find matrices A and B such that AB=O without either being zero. Therefore, statement (i) is false.
Step 2: Analyze Statement (ii)
Statement: AB=I2⇒A=B−1
Analysis:
This statement asserts that if the product of two matrices A and B is the identity matrix I2, then A must be the inverse of B.
Verification:
By definition, if AB=I2, then A is indeed the inverse of B (i.e., A=B−1). Therefore, statement (ii) is true.
Step 3: Analyze Statement (iii)
Statement: (A+B)2=A2+2AB+B2
Analysis:
This statement resembles the algebraic identity for the square of a binomial. However, matrix multiplication is not commutative, which means AB≠BA in general.
Counterexample:
Let:
A=(1000),B=(0100)
Calculating (A+B)2:
A+B=(1100)
(A+B)2=(1100)(1100)=(1100)
Now calculating A2+2AB+B2:
A2=(1000),B2=(0000),AB=(0100)
Thus,
A2+2AB+B2=(1000)+2(0000)+(0000)=(1000)
Since (A+B)2≠A2+2AB+B2, statement (iii) is false.
Conclusion
From the analysis:
- Statement (i) is false.
- Statement (ii) is true.
- Statement (iii) is false.
Thus, the correct option is (d): (i) and (iii) are false, (ii) is true.
Statement: AB=O⇒A=O or B=O
This statement claims that if the product of two matrices A and B is the zero matrix O, then at least one of the matrices must be the zero matrix.
Let:
A=(1000),B=(0001)
Calculating AB:
AB=(1000)(0001)=(0100)≠O
Now let’s take:
A=(1000),B=(0000)
Calculating AB:
AB=(1000)(0000)=(0000)=O
In this case, A≠O and B=O. However, we can also find matrices A and B such that AB=O without either being zero. Therefore, statement (i) is false.
Statement: AB=I2⇒A=B−1
This statement asserts that if the product of two matrices A and B is the identity matrix I2, then A must be the inverse of B.
By definition, if AB=I2, then A is indeed the inverse of B (i.e., A=B−1). Therefore, statement (ii) is true.
Statement: (A+B)2=A2+2AB+B2
This statement resembles the algebraic identity for the square of a binomial. However, matrix multiplication is not commutative, which means AB≠BA in general.
Let:
A=(1000),B=(0100)
Calculating (A+B)2:
A+B=(1100)
(A+B)2=(1100)(1100)=(1100)
Now calculating A2+2AB+B2:
A2=(1000),B2=(0000),AB=(0100)
Thus,
A2+2AB+B2=(1000)+2(0000)+(0000)=(1000)
Since (A+B)2≠A2+2AB+B2, statement (iii) is false.
From the analysis:
- Statement (i) is false.
- Statement (ii) is true.
- Statement (iii) is false.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Multiple Correct Answer49videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Linked Comprehension Type27videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - CAE 13.517videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
Similar Questions
Let A and B be two 2×2 matrices. Consider the statements (i) AB=0⇒A=0orB=0 (ii)AB=I2⇒A=B−1 (a) only (i) (b) only (ii) (c) both are correct (d) none of these.
View Solution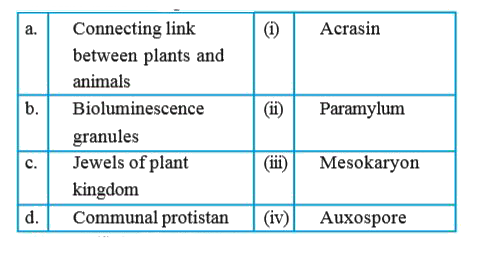
1 a(iii), b(ii), c(i), d(iv)
2 a(i), b(iv), c(i), d(iii)
3 a(iv), b(i), c(iii), d(iv)
4 a(ii), b(iii), c(iv), d(i)View SolutionIn Figure, which of the following statements must be true?
(i) a+b=d+c
(ii) a+c+e=1800
(iii) b+f=c+e
(a) (i) only
(b) (ii) only
(c) (iii) only
(d) (ii) and (iii) onlyView SolutionEvaluate : (i)(a+6b)2 (ii)(3x−4y)2 (iii)(2a−b+c)2
View SolutionConsider the following statements concerning a ΔABC
(i) The sides a,b,c and area of triangle are rational.
(ii) a,tanB2,tanC2
(iii) a,sinAsinB,sinC are rational .
Prove that (i)⇒(ii)⇒(iii)⇒(i)View SolutionIf a=2andb=−2, find the value of :
(i) a2+b2
(ii) a2+ab+b2
(iii) a2−b2View SolutionSubtract : (i) −5y2 from y2 (ii) 6xy from (iii) (a−b) from (a+b)
View SolutionBiodiversity loss occurs due to
(i) habitat loss and fragmentation
(ii) co-extinction
(iii) over-exploitation
(iv) alien species invasion.
(a) (i) and (ii)
(b) (i), (ii) and (iii)
(c) (ii), (iii) and (iv)
(d) (i), (ii), (iii) and (iv)View SolutionExpand the following
(i) (4a−b+ac)2 (ii) (3a−5b−c)2
(iii) (−x+2y−3z)2View SolutionMatch Column - I with Column - II and select the CORRECT option form the codes given below
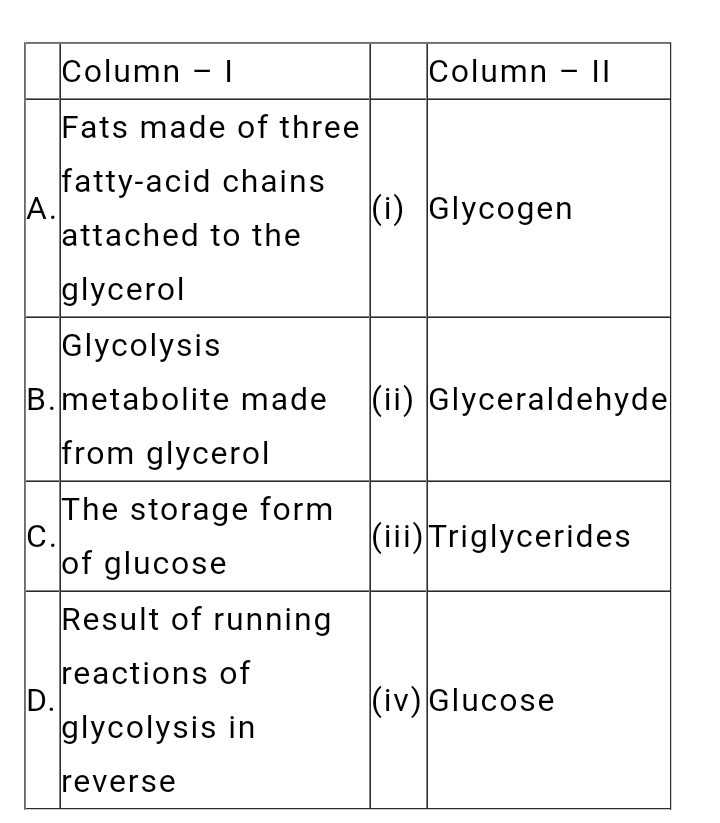
(a) A - (iv) , B - (ii) , C - (i) , D - (iii)
(b) A - (iii) , B - (ii) , C - (i) , D - (iv)
(c) A - (iv) , B - (iii) , C - (i) , D - (ii)
(d) A - (i) , B - (ii) , C - (iii) , D - (iv)View Solution

