Given a tetrahedrone D−ABC with AB=12,CD=6. If the shortest distance between the skew lines ABandCD is 8 and angle between them is π6, then find the volume of tetrahedron.
To find the volume of the tetrahedron D−ABC given the lengths of the edges and the distance between the skew lines, we can follow these steps:
Step 1: Identify the given data
- Length of line segment AB=12
- Length of line segment CD=6
- Shortest distance between lines AB and CD=8
- Angle between lines AB and CD=π6
Step 2: Understand the geometry of the tetrahedron
The tetrahedron consists of the triangular base ABC and the apex D. The lines AB and CD are skew lines, meaning they do not intersect and are not parallel.
Step 3: Calculate the area of triangle ABE
To find the area of triangle ABE, we can use the formula:
Area=12×AB×h×sin(θ)
where h is the height from point C to line AB and θ is the angle between the lines.
However, since we are looking for the area of triangle ABE in terms of the given lengths and angle, we can consider the height from C to line AB as the distance between the skew lines, which is given as 8.
Step 4: Calculate the area of triangle ABE
Using the formula:
Area=12×AB×CD×sin(θ)
Substituting the values:
Area=12×12×6×sin(π6)
Since sin(π6)=12:
Area=12×12×6×12=722=36
Step 5: Calculate the volume of the tetrahedron
The volume V of the tetrahedron is given by:
V=13×Area of base×height
Here, the area of the base triangle ABE is 36 and the height is the distance between the skew lines, which is 8:
V=13×36×8=2883=96
Step 6: Conclusion
Thus, the volume of the tetrahedron D−ABC is 96 cubic units.
- Length of line segment AB=12
- Length of line segment CD=6
- Shortest distance between lines AB and CD=8
- Angle between lines AB and CD=π6
The tetrahedron consists of the triangular base ABC and the apex D. The lines AB and CD are skew lines, meaning they do not intersect and are not parallel.
To find the area of triangle ABE, we can use the formula:
Area=12×AB×h×sin(θ)
where h is the height from point C to line AB and θ is the angle between the lines.
Using the formula:
Area=12×AB×CD×sin(θ)
Substituting the values:
Area=12×12×6×sin(π6)
Since sin(π6)=12:
Area=12×12×6×12=722=36
The volume V of the tetrahedron is given by:
V=13×Area of base×height
Here, the area of the base triangle ABE is 36 and the height is the distance between the skew lines, which is 8:
V=13×36×8=2883=96
Thus, the volume of the tetrahedron D−ABC is 96 cubic units.
Topper's Solved these Questions
Similar Questions
The lengths of two opposite edges of a tetrahedron are a and b; the shortest distane between these edges is d, and the angel between them is θ Prove using vectors that the volume of the tetrahedron is abdsinθ6 .
View SolutionThe lengths of two opposite edges of a tetrahedron of aandb; the shortest distane between these edgesis d, and the angel between them if θ. Prove using vector4s that the volume of the tetrahedron is abdisnθ6 .
View Solution
Knowledge Check
In the given figure, two lines AB and CD intersect at a point O. If ∠AOC+∠BOD=70∘, find the measure of ∠AOD
 A∠AOD=145∘B∠AOD=140∘C∠AOD=135∘D∠AOD=105∘
A∠AOD=145∘B∠AOD=140∘C∠AOD=135∘D∠AOD=105∘
Find the distance between the origin and the point :
(-8, 6)
View SolutionThe length of two opposite edges of a tetrahedron are 12 and 15 units and the shortest distance between them is 10 units. If the volume of the tetrahedron is 200 cubic units, then the angle between the 2 edges is
View SolutionIn the given figure if AB|| CD find ∠APMandPQD

View SolutionIF a=x2−2x+4x2+2x+4 and equation of lines AB and CD be 3y=xandy=3x respectively, then for all real x, point P(a,a2) (A) lies in the acute angle between lines AB and CD (B) lies in the obtuse angle between lines AB and CD (C) cannot be in the acute angle between lines AB and CD (D) cannot lie in the obtuse angle between lines AB and CD
View SolutionIn the given diagram 'O is the centre of the circle and AB is parallel to CD. AB = 24 cm and distance between he chord AB and CD is 17 cm. It the radius of the circle is 13 cm, find the length of the chord CD.
View SolutionLet ABCD be a trapezium ,in which AB is parallel to CD, AB =11 ,BC=4,CD=6 and DA=3. the distance between AB and CD is
View SolutionIn the figure if EC is the bisector of ∠BCDandAB||CD||EF. Find ∠ABC
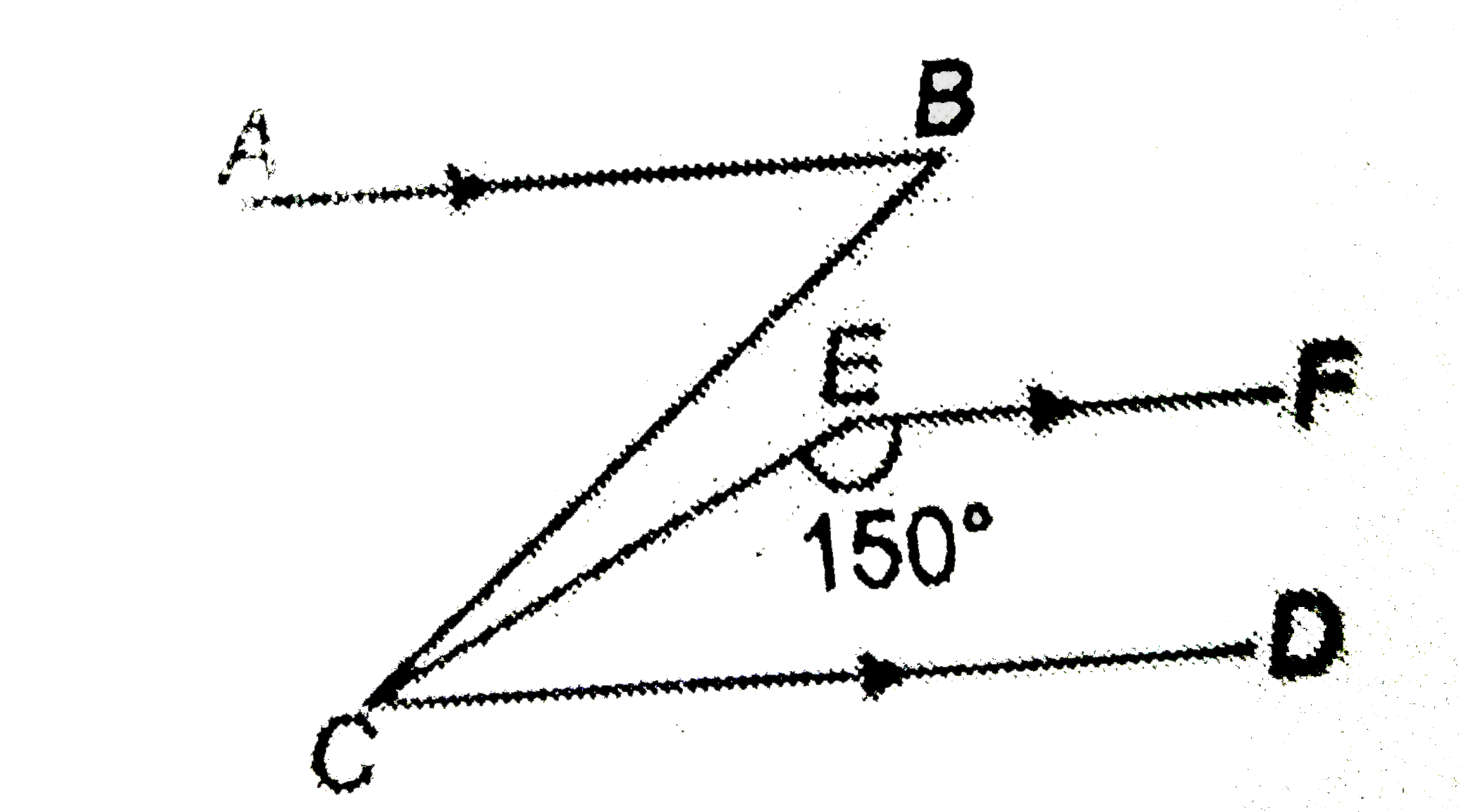
View Solution