Let AB is the focal chord of a parabola and D and C be the foot of the perpendiculars from A and B on its directrix respectively. If CD = 6 units and area of trapezium ABCD is 36 square units, then the length (in units) of the chord AB is
Step by step video solution for Let AB is the focal chord of a parabola and D and C be the foot of the perpendiculars from A and B on its directrix respectively. If CD = 6 units and area of trapezium ABCD is 36 square units, then the length (in units) of the chord AB is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A point P on the parabola y2=4x, the foot of the perpendicular from it upon the directrix and the focus are the vertices of an equilateral triangle. If the area of the equilateral triangle is β sq. units, then the value of β2 is
View SolutionA point on a parabola y2=4ax, the foot of the perpendicular from it upon the directrix, and the focus are the vertices of an equilateral triangle. The focal distance of the point is equal to a2 (b) a (c) 2a (d) 4a
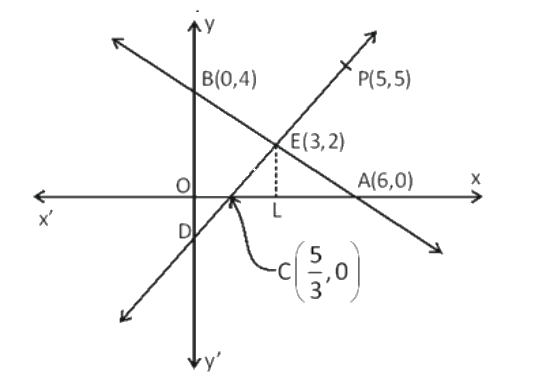
View SolutionThe line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
View SolutionAB is a chord of the parabola y2=4ax with its vertex at A. BC is drawn perpendicular to AB meeting the axis at C.The projecton of BC on the axis of the parabola is
View SolutionAB is a chord of the parabola y2=4ax with its vertex at A. BC is drawn perpendicular to AB meeting the axis at C.The projecton of BC on the axis of the parabola is
View SolutionIn the adjoining figure, 'O' is the centre of the circle. OL and OM are perpendiculars from O to the chords AB and CD respectively. If OL=OM and AB=16cm, then find the length of CD.

View SolutionProve that the length of a focal chord of a parabola varies inversely as the square of its distance from the vertex.
View SolutionTangents are drawn from any point on the directrix of y2=16x to the parabola. If thelocus of the midpoint of chords of contact is a parabola, then its length (in units) of the latus rectum is
View SolutionLet ABCD be a parallelogram the equation of whose diagonals are AC:x+2y=3; BD:2x+y=3. If length of diagonal AC=4 units and area of ABCD=8 sq. units. Then
(i) The length of the other diagonal is
(ii) the length of side AB is equal to
View SolutionIf the length of a focal chord of the parabola y2=4ax at a distance b from the vertex is c, then prove that b2c=4a3.
View Solution
